题目内容
2.已知直线l1:ax-y+1=0,l2:x+y+1=0,l1∥l2,则a的值为-1,直线l1与l2间的距离为$\sqrt{2}$.分析 利用两条直线相互平行的充要条件即可得出.
解答 解:直线l1:ax-y+1=0,l2:x+y+1=0,分别化为:y=ax+1,y=-x-1,
∵l1∥l2,∴a=-1,1≠-1.
两条直线方程可得:x+y-1=0,x+y+1=0.
直线l1与l2间的距离d=$\frac{|-1-1|}{\sqrt{2}}$=$\sqrt{2}$.
故答案分别为:-1;$\sqrt{2}$.
点评 本题考查了两条直线相互平行的充要条件,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
11.已知向量$\overrightarrow{m}$=(1,cosθ),$\overrightarrow{n}$=(sinθ,-2),且$\overrightarrow{m}$⊥$\overrightarrow{n}$,则sin2θ+6cos2θ的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | -2 |
12.已知数列{bn}满足b1=$\frac{1}{2}$,2bn+1-bn•bn+1=1,则b1+$\frac{{b}_{2}}{{2}^{2}}$+$\frac{{b}_{3}}{{3}^{2}}$+…+$\frac{{b}_{100}}{10{0}^{2}}$=( )
| A. | $\frac{97}{100}$ | B. | $\frac{99}{100}$ | C. | $\frac{100}{101}$ | D. | $\frac{102}{101}$ |
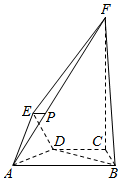 如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.
如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.