题目内容
已知函数f(x)=x2+2mx+2m+3(m∈R),若关于x的方程f(x)=0有实数根,且两根分别为x1、x2,
(1)求(x1+x2)•x1x2的最大值;
(2)若函数f(x)为偶函数,证明:函数g(x)=
在[2,3]上的单调性.
(1)求(x1+x2)•x1x2的最大值;
(2)若函数f(x)为偶函数,证明:函数g(x)=
| f(x) |
| x |
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:(1)由韦达定理可得x1+x2=-2m;x1x2=2m+3;从而化简(x1+x2)•x1x2=-2m(2m+3)=-4(m+
)2+
;再由△≥0解出m的取值范围,从而求最值;
(2)由题意可得m=0;故g(x)=
=x+
;从而由定义法证明函数的单调性.
| 3 |
| 4 |
| 9 |
| 4 |
(2)由题意可得m=0;故g(x)=
| f(x) |
| x |
| 3 |
| x |
解答:
解:(1)由题意,
x1+x2=-2m;x1x2=2m+3;
(x1+x2)•x1x2=-2m(2m+3)=-4(m+
)2+
;
又∵△=4m2-4(2m+3)≥0;
∴m≤-1或m≥3,
∵t=-4(m+
)2+
在m∈(-∞,-1]上单调递增,
m=-1时最大值为2,
t=-4(m+
)2+
在m∈[3,+∞)上单调递减,
m=3时最大值为-54,
∴(x1+x2)•x1x2的最大值为2.
(2)证明:因为函数f(x)为偶函数,所以m=0,
g(x)=
=x+
;
任取2≤x1<x2≤3,
则f(x2)-f(x1)=x2+
-(x1+
)
=(x2-x1)
>0;
故g(x)在[2,3]上递增.
x1+x2=-2m;x1x2=2m+3;
(x1+x2)•x1x2=-2m(2m+3)=-4(m+
| 3 |
| 4 |
| 9 |
| 4 |
又∵△=4m2-4(2m+3)≥0;
∴m≤-1或m≥3,
∵t=-4(m+
| 3 |
| 4 |
| 9 |
| 4 |
m=-1时最大值为2,
t=-4(m+
| 3 |
| 4 |
| 9 |
| 4 |
m=3时最大值为-54,
∴(x1+x2)•x1x2的最大值为2.
(2)证明:因为函数f(x)为偶函数,所以m=0,
g(x)=
| f(x) |
| x |
| 3 |
| x |
任取2≤x1<x2≤3,
则f(x2)-f(x1)=x2+
| 3 |
| x2 |
| 3 |
| x1 |
=(x2-x1)
| x1x2-3 |
| x1x2 |
故g(x)在[2,3]上递增.
点评:本题考查了二次函数的性质应用及单调性与最值的求法,属于中档题.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
已知P是抛物线y2=4x上一动点,则点P到直线l:2x-y+3=0和y轴的距离之和的最小值是( )
A、
| ||
B、
| ||
| C、2 | ||
D、
|
已知函数f(x)=
,设b>a≥0,若f(a)=f(b),则a•f(b)的取值范围是( )
|
A、[-
| ||||
B、[-
| ||||
C、[
| ||||
D、[
|
某学校用800元购买A,B两种教学用品,A种用品每件100元,B种用品每件160元,两种用品至少各买一件,要使剩下的钱最少,A,B两种用品应各买的件数为( )
| A、2件,4件 | B、3件,3件 |
| C、4件,2件 | D、不确定 |
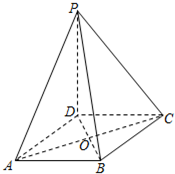 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形