题目内容
给定正数a，b，且a＜b，设An=
，n∈N*．
（1）比较A1，A2，A3的大小；
（2）由（1）猜想数列{An}的单调性，并给出证明．
| a+nb |
| 1+n |
（1）比较A1，A2，A3的大小；
（2）由（1）猜想数列{An}的单调性，并给出证明．
考点：数列的函数特性,数列递推式
专题：点列、递归数列与数学归纳法
分析：（1）由An=
，n∈N*，正数a＜b，可求得A1，A2，A3，分别作差比较即可；
（2）由（1）可猜想数列{An}为单调递增数列，再对An+1与An作差An+1-An，判断即可．
| a+nb |
| 1+n |
（2）由（1）可猜想数列{An}为单调递增数列，再对An+1与An作差An+1-An，判断即可．
解答：
解：（1）∵An=
，n∈N*．
∴A1=
，
A2=
=
，
A3=
，
又a＜b，
∴A1-A2=
-
=
＜0，即A1＜A2；
同理可得，A2-A3=
＜0，即A2＜A3；
∴A1＜A2＜A3；
（2）由（1）可猜想数列{An}为单调递增数列．
∵An+1-An=
-
=
=
＞0，
∴An+1＞An，
即数列{An}为单调递增数列．
| a+nb |
| 1+n |
∴A1=
| a+b |
| 2 |
A2=
| a+2b |
| 1+2 |
| a+2b |
| 3 |
A3=
| a+3b |
| 4 |
又a＜b，
∴A1-A2=
| a+b |
| 2 |
| a+2b |
| 3 |
| a-b |
| 6 |
同理可得，A2-A3=
| a-b |
| 12 |
∴A1＜A2＜A3；
（2）由（1）可猜想数列{An}为单调递增数列．
∵An+1-An=
| a+(n+1)b |
| 1+(n+1) |
| a+nb |
| 1+n |
| (n+1)[a+(n+1)b]-(n+2)(a+nb) |
| (n+2)(n+1) |
| b-a |
| (n+2)(n+1) |
∴An+1＞An，
即数列{An}为单调递增数列．
点评：本题考查数列递推式的应用，着重考查数列的函数特性，突出考查作差法的应用，属于中档题．
练习册系列答案
相关题目
如图，函数y=x+a，y=ax（a＞0，a≠1）的图象可能是（ ）
A、 |
B、 |
C、 |
D、 |
已知非零向量
，
满足向量
+
与向量
-
的夹角为
，那么下列结论中一定成立的是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 2 |
A、
| ||||
B、|
| ||||
C、
| ||||
D、
|
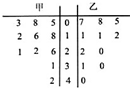某赛季，甲、乙两名篮球运动员都参加了11场比赛，他们在这11场比赛的得分用下面的茎叶图表示，设甲运动员得分的中位数为M1，乙运动员得分的中位数为M2，则在下列选项中，正确的是（ ）| A、M1=18，M2=11 |
| B、M1=81，M2=12 |
| C、M1=8，M2=2 |
| D、M1=3，M2=1 |