题目内容
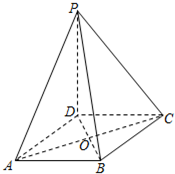如图，在四棱锥P-ABCD中，PD⊥平面ABCD，底面ABCD是菱形（Ⅰ）求证：AC⊥平面PBD；
（Ⅱ）若∠BAD=60°，AD=2，PD=2
| 2 |
考点：直线与平面所成的角,直线与平面垂直的判定
专题：空间位置关系与距离,空间角
分析：（Ⅰ）由已知得PD⊥AC，BD⊥AC，由此能证明AC⊥平面PBD．
（Ⅱ）连接PO，∠APO是PA与平面PBD所成的角，由此能求出PA与平面PBD所成角的大小．
（Ⅱ）连接PO，∠APO是PA与平面PBD所成的角，由此能求出PA与平面PBD所成角的大小．
解答：
（本小题10分）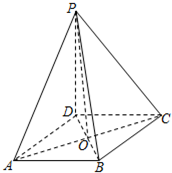
（Ⅰ）证明：∵PD⊥平面ABCD，∴PD⊥AC，
又ABCD是菱形，∴BD⊥AC，
∵PD∩BD=D，∴AC⊥平面PBD．…（5分）
（Ⅱ）解：连接PO．∵AC⊥平面PBD，
∴∠APO是PA与平面PBD所成的角．
又AD=2，AO=
，
PD=2
，PA=
=2
∴∠APO=30°．
∴PA与平面PBD所成角的大小为30°．…（10分）
（Ⅰ）证明：∵PD⊥平面ABCD，∴PD⊥AC，
又ABCD是菱形，∴BD⊥AC，
∵PD∩BD=D，∴AC⊥平面PBD．…（5分）
（Ⅱ）解：连接PO．∵AC⊥平面PBD，
∴∠APO是PA与平面PBD所成的角．
又AD=2，AO=
| 3 |
PD=2
| 2 |
| PD2+DA2 |
| 3 |
∴∠APO=30°．
∴PA与平面PBD所成角的大小为30°．…（10分）
点评：本题考查直线与平面垂直的证明，考查线面角的求法，是中档题，解题时要注意空间思维能力的培养．
练习册系列答案
相关题目
4名同学要在同一天上、下午到实验室做A，B，C，D，E五个操作实验，每个同学上下午各做一个实验，且不重复，若上午不能做D实验，下午不能做E实验，则不同的安排方式共有（ ）
| A、144种 | B、192种 |
| C、216种 | D、264种 |