题目内容
已知直线l:ax+by+c=0被圆C:x2+y2=10截得的弦的中点为M,若a+3b-c=0,O为坐标原点,则
(1)点M的轨迹方程为 ;
(2)|OM|的最大值为 .
(1)点M的轨迹方程为
(2)|OM|的最大值为
考点:直线与圆相交的性质
专题:直线与圆
分析:(1)根据直线和圆相交的性质,利用条件消去参数a,b,c即可得到结论.
(2)直线ax+by+c=0过定点N(-1,-3),根据点和圆的位置关系即可得到结论.
(2)直线ax+by+c=0过定点N(-1,-3),根据点和圆的位置关系即可得到结论.
解答:
解:(1)若直线l:ax+by+c=0被圆C:x2+y2=10截得的弦的中点为M,
则满足OM⊥l,
设M(x,y),
则
=
,即a=
,
∵a+3b-c=0,
∴c=a+3b=
+3b,
将a,c代入直线ax+by+c=0得
x+by+
+3b=0,
整理得x2+y2+x+3y=0,
故点M的轨迹方程为x2+y2+x+3y=0;
(2)∵M的轨迹方程为x2+y2+x+3y=0,a+3b-c=0,
∴-a-3b+c=0,
即直线l:ax+by+c=0过定点N(-1,-3),
而点N(-1,-3)在圆x2+y2=10上,
∴|OM|的最大值为
=
.
故答案为:x2+y2+x+3y=0,
.
则满足OM⊥l,
设M(x,y),
则
| y |
| x |
| b |
| a |
| bx |
| y |
∵a+3b-c=0,
∴c=a+3b=
| bx |
| y |
将a,c代入直线ax+by+c=0得
| bx |
| y |
| bx |
| y |
整理得x2+y2+x+3y=0,
故点M的轨迹方程为x2+y2+x+3y=0;
(2)∵M的轨迹方程为x2+y2+x+3y=0,a+3b-c=0,
∴-a-3b+c=0,
即直线l:ax+by+c=0过定点N(-1,-3),
而点N(-1,-3)在圆x2+y2=10上,
∴|OM|的最大值为
| (1-0)2+(3-0)2 |
| 10 |
故答案为:x2+y2+x+3y=0,
| 10 |
点评:本题主要考查与圆有关的轨迹问题.利用直线和圆的位置关系是解决本题的关键.

练习册系列答案
相关题目
数列{an}满足a1=2,an=
,其前n项积Tn,则T2015=( )
| an+1-1 |
| an+1+1 |
| A、1 | B、-6 | C、2 | D、3 |
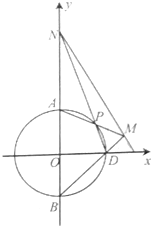 如图所示,已知圆C:x2+y2=r2(r>0)上点
如图所示,已知圆C:x2+y2=r2(r>0)上点