题目内容
14.若cos($\frac{π}{2}+α$)=$\frac{3}{5}$,则cos2α=( )| A. | $-\frac{7}{25}$ | B. | $\frac{7}{25}$ | C. | 一$\frac{16}{25}$ | D. | $\frac{16}{25}$ |
分析 由已知利用诱导公式可求sinα的值,进而利用二倍角的余弦函数公式即可计算得解.
解答 解:∵cos($\frac{π}{2}+α$)=$\frac{3}{5}$,可得:-sinα=$\frac{3}{5}$,
∴sinα=-$\frac{3}{5}$,
∴cos2α=1-2sin2α=1-2×(-$\frac{3}{5}$)2=$\frac{7}{25}$.
故选:B.
点评 本题主要考查了诱导公式,二倍角的余弦函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.若圆C1:(x-a)2+y2=4与圆C2:x2+(y-$\sqrt{5}$)2=a2相外切,则实数a的值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{4}$或-$\frac{1}{4}$ | C. | $\frac{1}{2}$或-$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
19.某几何体的三视图如图所示,则该几何体的外接球的半径为( )
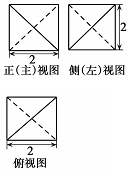

| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | $\sqrt{2}$ |
6.若复数$z=\frac{1-i}{i}$(i为虚数单位),则z的共轭复数$\overline z$=( )
| A. | 1+i | B. | -1+i | C. | l-i | D. | -1一i |
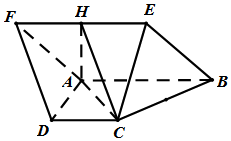 如图所示,菱形ABEF⊥直角梯形ABCD,∠BAD=∠CDA=90°,∠ABE=60°,AB=2AD=2CD=2,H是EF的中点
如图所示,菱形ABEF⊥直角梯形ABCD,∠BAD=∠CDA=90°,∠ABE=60°,AB=2AD=2CD=2,H是EF的中点