题目内容
6.若复数$z=\frac{1-i}{i}$(i为虚数单位),则z的共轭复数$\overline z$=( )| A. | 1+i | B. | -1+i | C. | l-i | D. | -1一i |
分析 利用复数的运算法则、共轭复数的定义即可得出.
解答 解:复数$z=\frac{1-i}{i}$=$\frac{-i(1-i)}{-i•i}$=-i-1,则z的共轭复数$\overline z$=-1+i.
故选:B.
点评 本题考查了复数的运算法则、共轭复数的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
16.$cos(-\frac{19π}{6})$的值为.( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
17.过点P(2,-1)且倾斜角为$\frac{π}{4}$的直线方程是( )
| A. | x-y+1=0 | B. | $\sqrt{2}$x-2y-$\sqrt{2}$-2=0 | C. | x-y-3=0 | D. | $\sqrt{2}$x-2y+$\sqrt{2}$+1=0 |
14.若cos($\frac{π}{2}+α$)=$\frac{3}{5}$,则cos2α=( )
| A. | $-\frac{7}{25}$ | B. | $\frac{7}{25}$ | C. | 一$\frac{16}{25}$ | D. | $\frac{16}{25}$ |
11.阅读如图的程序框图,运行相应的程序,则输出的值为( )
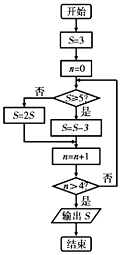

| A. | 3 | B. | 4 | C. | 6 | D. | 7 |
15.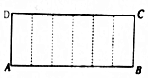 已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为( )
已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为( )
 已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为( )
已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为( )| A. | 13π | B. | 12π | C. | 11π | D. | 10π |
16.已知函数f(x)=lgx,0<a<b,若p=f($\sqrt{ab}$),q=f($\frac{a+b}{2}$),r=$\frac{1}{2}$[f(a)+f(b)],则p,q,r的大小关系是( )
| A. | p=r>q | B. | p=r<q | C. | q=r<p | D. | q-r>p |