题目内容
11.函数f(x)=sin(5x+$\frac{π}{4}$)的图象的对称中心是($\frac{1}{5}$kπ-$\frac{π}{20}$,0)k∈Z.分析 根据正弦函数的对称中心方程,求出函数的图象的对称中心即可.
解答 解:因为5x+$\frac{π}{4}$=kπ,k∈Z,所以x=$\frac{1}{5}$kπ-$\frac{π}{20}$,k∈Z,
所以函数y=sin(5x+$\frac{π}{4}$)的图象的对称中心:($\frac{1}{5}$kπ-$\frac{π}{20}$,0)k∈Z,
故答案为:($\frac{1}{5}$kπ-$\frac{π}{20}$,0)k∈Z.
点评 本题是基础题,考查正弦函数的对称性,能够利用基本函数的性质求解函数的有关性质,是高考常考题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
6.“x2+2x-3=0”是“x=1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.设P(x0,y0)是函数f(x)图象上任意一点,且$y_0^2≥x_0^2$,则f(x)的解析式可以是( )
| A. | $f(x)=x-\frac{1}{x}$ | B. | f(x)=ex-1 | C. | $f(x)=x+\frac{4}{x}$ | D. | f(x)=tanx |
7.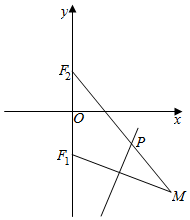 如图所示,点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.当点M变化时,则动点P的轨迹方程为( )
如图所示,点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.当点M变化时,则动点P的轨迹方程为( )
 如图所示,点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.当点M变化时,则动点P的轨迹方程为( )
如图所示,点F1(0,-$\sqrt{2}$),F2(0,$\sqrt{2}$),动点M到点F2的距离是4,线段MF1的中垂线交MF2于点P.当点M变化时,则动点P的轨迹方程为( )| A. | $\frac{x^2}{4}+\frac{y^2}{2}=1$ | B. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{2}$=1 | C. | x2+y2=1 | D. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ |
