题目内容

2．已知函数f（x）=$\left\{\begin{array}{l}{\sqrt{x}，x＞0}\\{{2}^{-x}，x≤0}\end{array}\right.$，则f[f（-4）]=4．

分析 利用分段函数，逐步求解函数值即可．

解答 解：函数f（x）=$\left\{\begin{array}{l}{\sqrt{x}，x＞0}\\{{2}^{-x}，x≤0}\end{array}\right.$，
则f[f（-4）]=f（24）=$\sqrt{{2}^{4}}$=4．
故答案为：4．

点评 本题考查函数值的求法，考查分段函数的应用，考查计算能力．

练习册系列答案
相关题目
6．“x2+2x-3=0”是“x=1”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
13．已知$a={log_{\frac{1}{3}}}\frac{1}{2}$，b=log23，c=log34，则（　　）
A．a＞b＞cB．b＞a＞cC．c＞b＞aD．b＞c＞a
10．设函数f（x）=|x-3|+|x+7|．
（1）解不等式：f（x）＜16；
（2）若存在x0∈R，使f（x0）＜a，求实数a的取值范围．
17．已知△ABC的顶点A、B的坐标分别为（-$\sqrt{3}$，0）、（$\sqrt{3}$，0），C为动点，且满足sinB+sinA=$\sqrt{2}$sinC．
（1）求点C的轨迹L的方程；
（2）设M（x0，y0）是曲线L上的任一点，从原点O向圆M：（x-x0）2+（y-y0）2=2作两条切线，分别交曲线L于点P、Q．
①若直线OP、OQ的斜率均存在，并记为k1，k2，求证：k1k2为定值；
②试问OP2+OQ2是否为定值？若是，求出该值；若不是，请说明理由．
7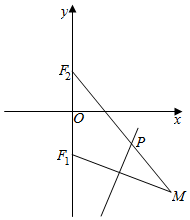．如图所示，点F1（0，-$\sqrt{2}$），F2（0，$\sqrt{2}$），动点M到点F2的距离是4，线段MF1的中垂线交MF2于点P．当点M变化时，则动点P的轨迹方程为（　　）
A．$\frac{x^2}{4}+\frac{y^2}{2}=1$B．$\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{2}$=1C．x2+y2=1D．$\frac{y^2}{4}-\frac{x^2}{2}=1$
14．复数$\frac{2i}{1-i}$（i是虚数单位）的虚部是（　　）
A．-1B．2C．-2D．1
11．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，满足$\overrightarrow{a}$=（1，3），（$\overrightarrow{a}$+$\overrightarrow{b}$）⊥（$\overrightarrow{a}$-$\overrightarrow{b}$），则|$\overrightarrow{b}$|=$\sqrt{10}$．
12．在△ABC中，角A，B，C的对边分别为a，b，c，已知2ccosB=2a-b．
（Ⅰ）求角C的大小；
（Ⅱ）若$c=\sqrt{3}$，b-a=1，求△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网