题目内容
17．已知函数f（x）为奇函数，当x≥0时，f（x）=log2（x+l）+m，则f（1-$\sqrt{2}$）的值为（ ）| A． | -$\frac{1}{2}$ | B． | -log2（2-$\sqrt{2}$） | C． | $\frac{1}{2}$ | D． | log2（2-$\sqrt{2}$） |
分析 根据函数奇偶性的性质，利用f（0）=0，先求出m，然后代入即可．
解答 解：函数f（x）为奇函数，当x≥0时，f（x）=log2（x+l）+m，
∴f（0）=log2l+m=0，则m=0，
则f（1-$\sqrt{2}$）=-f（$\sqrt{2}$-1）=-log2（$\sqrt{2}$-1+l）=-log2$\sqrt{2}$=-$\frac{1}{2}$，
故选：A．
点评 本题主要考查函数值的计算，根据函数奇偶性的性质进行转化是解决本题的关键．
练习册系列答案
相关题目
7．
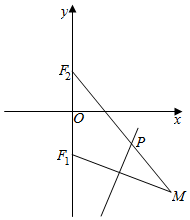如图所示，点F1（0，-$\sqrt{2}$），F2（0，$\sqrt{2}$），动点M到点F2的距离是4，线段MF1的中垂线交MF2于点P．当点M变化时，则动点P的轨迹方程为（ ）
如图所示，点F1（0，-$\sqrt{2}$），F2（0，$\sqrt{2}$），动点M到点F2的距离是4，线段MF1的中垂线交MF2于点P．当点M变化时，则动点P的轨迹方程为（ ）| A． | $\frac{x^2}{4}+\frac{y^2}{2}=1$ | B． | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{2}$=1 | C． | x2+y2=1 | D． | $\frac{y^2}{4}-\frac{x^2}{2}=1$ |
5．若集合A=[2，3]，B={x|x2-5x+6=0|，则A∩B=（ ）
| A． | {2，3} | B． | ∅ | C． | 2 | D． | [2，3] |
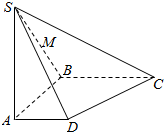如图，在底面是直角梯形的四棱锥S-ABCD中，∠ABC=∠DAB=90°，SA⊥平面ABCD，SA=AB=BC=2，AD=1，M为SB的中点，过点M、A、D的截面MADN交SC于点N．
9．奇函数f（x）的定义域为R，若f（x+1）为偶函数，且f（1）=2，则f（4）+f（5）的值为（ ）
| A． | 2 | B． | 1 | C． | -1 | D． | -2 |