题目内容
已知x,y满足不等式组
,若y-ax<3恒成立,则实数a的取值范围为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用线性规划的知识进行求解即可.
解答:
解:作出不等式组对应的平面区域如图: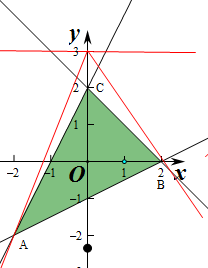
若y-ax<3恒成立即y<ax+3恒成立,
即平面区域ABC在直线y=ax+3的下方即可.
即A,B(2,0)在y=ax+3的下方即可,
由
解得
,即A(-2,-2).
即
,
即
,
解得-
<a<
,
故答案为:(-
,
)

若y-ax<3恒成立即y<ax+3恒成立,
即平面区域ABC在直线y=ax+3的下方即可.
即A,B(2,0)在y=ax+3的下方即可,
由
|
|
即
|
即
|
解得-
| 3 |
| 2 |
| 5 |
| 2 |
故答案为:(-
| 3 |
| 2 |
| 5 |
| 2 |
点评:本题主要考查线性规划的应用,根据条件y-ax<3恒成立,得到平面区域ABC在直线y=ax+3的下方是解决本题的关键.

练习册系列答案
相关题目
定义在R上的函数f(x)满足:f(x+1)=-f(x),且当x∈(0,1)时,f(x)=2x-1,则f(log220)的值为( )
A、
| ||
B、
| ||
C、
| ||
D、-
|
若a,b,c是空间三条直线,β是一个平面,下列命题正确的是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
下列说法错误的是( )
| A、“x>1”是“|x|>1”的充分不必要条件 |
| B、若p且q为假命题,则p、q均为假命题 |
| C、命题“若x2-4x+3=0,则x=3”的逆否命题是:“若x≠3,则x2-4x+3≠0” |
| D、命题p:“?x∈R,使得x2+x+1<0”,则?p:“?x∈R,均有x2+x+1≥0” |
已知向量
=(-4,3),点A(-1,1)和B(0,-1)在
上的射影分别为A1和B1,若
=λ
,则λ的值是( )
| a |
| a |
| A1B1 |
| a |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
已知定义在R上的可导函数y=f(x)是偶函数,且满足xf′(x)<0,f(
)=0,则满足f(log
x)<0的x的范围为( )
| 1 |
| 2 |
| 1 |
| 4 |
A、(-∞,
| ||
B、(
| ||
C、(
| ||
D、(0,
|