题目内容
7.已知函数f(x)=ax3+$\frac{3}{2}$x2sinθ-6x+1,且对任意的实数t,恒有f′(-e${\;}^{{t}^{2}}$)≥0,f′(3|cost|-1)≤0.(1)求函数f(x)的解析式;
(2)对?x1,x2∈[0,3],求证:|f(x1)-f(x2)|≤10.
分析 (1)求函数的导数,根据条件,建立方程或不等式结合三角函数的有界性即可求函数f(x)的解析式;
(2)对?x1,x2∈[0,3],不等式|f(x1)-f(x2)|≤10等价为:|f(x1)-f(x2)|≤|f(x)max-f(x)min|,利用导数求出函数的最值即可..
解答 解:(1)函数的导数f′(x)=3ax2+3xsinθ-6,
∵-e${\;}^{{t}^{2}}$≤-1,∵3|cost|-1∈[2,4],
∴对任意的实数t,恒有f′(-e${\;}^{{t}^{2}}$)≥0,f′(3|cost|-1)≤0.
∴当t=0时,f′(-e${\;}^{{t}^{2}}$)=f′(-1)≥0,
当cost=0时,f′(3|cost|-1)=f′(-1)≤0,即f′(-1)=0,
∴等价为$\left\{\begin{array}{l}{f′(-1)=0}\\{f′(2)≤0}\end{array}\right.$,即$\left\{\begin{array}{l}{f′(-1)=3a-3sinθ-6=0}\\{12a+6sinθ-6≤0}\end{array}\right.$,即$\left\{\begin{array}{l}{a-sinθ-2=0}\\{2a+sinθ-1≤0}\end{array}\right.$,
消去a或sinθ得3sinθ≤-3,
∴sinθ=-1,a=1,
则f(x)=x3-$\frac{3}{2}$x2-6x+1.
(2)f′(x)=3x2-3x-6=3(x+1)(x-2),
由f′(x)=0,则x=-1或x=2.
当x变化时,f′(x)和f(x)的变化如表:
| x | 0 | (0,2) | 2 | (2,3) | 3 |
| f′(x) | - | + | |||
| f(x) | 1 | 递减 | -9 | 递增 | -$\frac{7}{2}$ |
则:|f(x1)-f(x2)|≤|f(x)max-f(x)min|=|1-(-9)|=10.
即|f(x1)-f(x2)|≤10成立.
点评 本题主要考查函数解析式的求解以及函数最值的求解,求函数的导数,利用导数研究函数的单调性和最值是解决本题的关键.

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案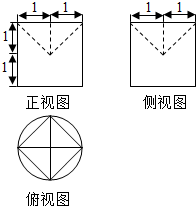
| A. | 2π-$\frac{2}{3}$ | B. | 2π-$\frac{4}{3}$ | C. | $\frac{5π}{3}$ | D. | 2π-2 |
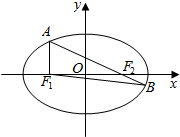 如图,点F1,F2分别是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点.点A是椭圆C上一点,点B是直线AF2与椭圆C的另一交点,且满足AF1⊥x轴,∠AF2F1=30°.
如图,点F1,F2分别是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点.点A是椭圆C上一点,点B是直线AF2与椭圆C的另一交点,且满足AF1⊥x轴,∠AF2F1=30°. 在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和A1B1的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和A1B1的中点.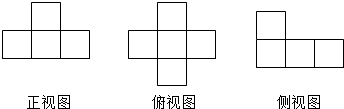
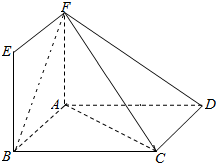 在如图所示的几何体中,四边形ABCD为平行四边形,平面ABEF⊥平面ABCD,∠ACD=90°,AB=2,AD=4,ABEF为正方形,平面ABEF⊥平面ABCD,AN⊥CF,垂足为N.
在如图所示的几何体中,四边形ABCD为平行四边形,平面ABEF⊥平面ABCD,∠ACD=90°,AB=2,AD=4,ABEF为正方形,平面ABEF⊥平面ABCD,AN⊥CF,垂足为N.