题目内容
将一个白球，两个相同的红球，三个相同的黄球摆放成一排．则白球与黄球不相邻的放法有（ ）
| A、10种 | B、12种 |
| C、14种 | D、16种 |
考点：排列、组合及简单计数问题
专题：排列组合
分析：根据分类计数原理分两类，当白球在两端时，当白球不在两端时，问题得以解决．
解答：
解：当白球在两端时，和白球相邻的必须是红球，另一个红球插入三个相同的黄球和红球所形成的间隔中，共有2
=8种，
当白球不在两端时，则白球必须在两个红球之间，把两个红球夹一个白球看做一个元素，然后插入三个相同的黄球所形成的间隔中，共有
=4种，
根据分类计数原理分两类，白球与黄球不相邻的放法共有8+4=12种．
故选：B．
| A | 1 4 |
当白球不在两端时，则白球必须在两个红球之间，把两个红球夹一个白球看做一个元素，然后插入三个相同的黄球所形成的间隔中，共有
| A | 1 4 |
根据分类计数原理分两类，白球与黄球不相邻的放法共有8+4=12种．
故选：B．
点评：本题主要考查了分类计数原理，根据不重不漏的原则是分类是关键，属于中档题．
练习册系列答案
相关题目
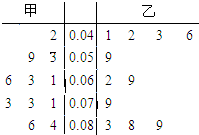PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．根据北京某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据（单位：毫克/每立方米）列出的茎叶图，如图，则甲、乙两地所测数据的中位数较低的是（ ）| A、甲 | B、乙 |
| C、甲乙相等 | D、无法确定 |
| cos2600° |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
长方体的表面积是24，所有棱长的和是24，则对角线的长是（ ）
A、
| ||
| B、4 | ||
C、3
| ||
D、2
|
高二年级计划从3名男生和4名女生中选3人参加某项会议，则选出的3人中既有男生又有女生的选法种数为（ ）
| A、24 | B、30 | C、60 | D、90 |
已知m、n、l为直线，α、β、γ为平面，下列命题为真命题的是（ ）
| A、若m∥α，m∥β，则α∥β |
| B、若m?α，n?β，α⊥β，则m⊥n |
| C、若l⊥n，l⊥m，m?α，n?α，则l⊥α |
| D、若α⊥β，α∥γ，则β⊥γ |
复数
的共轭复数对应的点在复平面的（ ）
| 5 |
| i-2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
三角形面积为S=
（a+b+c）r，a，b，c为三角形三边长，r为三角形内切圆半径，利用类比推理，可以得出四面体的体积为（ ）
| 1 |
| 2 |
A、V=
| ||
B、V=
| ||
C、V=
| ||
D、V=
|