题目内容
已知盒中装有3个红球、2个白球、5个黑球，它们大小形状完全相同，现需一个红球，甲每次从中任取一个不放回，在他第一次拿到白球的条件下，第二次拿到红球的概率（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：条件概率与独立事件
专题：概率与统计
分析：利用条件概率公式，设“第一次拿到白球”为事件A，“第二次拿到红球”为事件B，分别求出P（A），P（AB），根据条件概率公式求得即可．
解答：
解：设“第一次拿到白球”为事件A，“第二次拿到红球”为事件B
∴P（A）=
=
，P（A•B）=
×
=
则所求概率为P（B|A）=
=
=
故选：B．
∴P（A）=
| 2 |
| 10 |
| 1 |
| 5 |
| 1 |
| 5 |
| 3 |
| 9 |
| 1 |
| 15 |
则所求概率为P（B|A）=
| P(A•B) |
| P(A) |
| ||
|
| 1 |
| 3 |
故选：B．
点评：本题主要考查条件概率的求法，熟练掌握条件概率的概率公式是关键．
练习册系列答案
相关题目
在空间内，设l，m，n是三条不同的直线，α，β，γ是三个不同的平面，则下列命题中为假命题的是（ ）
| A、α⊥γ，β⊥γ，α∩β=l，则l⊥γ |
| B、l∥α，l∥β，α∩β=m，则l∥m |
| C、α∩β=l，β∩γ=m，γ∩α=n，l∥m，则l∥n |
| D、α⊥γ，β⊥γ，则α⊥β或α∥β |
函数y=sin2x-3cosx+2的最小值为（ ）
| A、5 | B、0 | C、2 | D、-1 |
已知不等式x2-x≤0的解集为M，且集合N={x|
＜0}，则M∩N为（ ）
| x+1 |
| x-1 |
| A、[0，1） |
| B、（0，1） |
| C、[0，1] |
| D、（-1，0] |
下列说法正确的是（ ）
| A、命题“若am2＜bm2，则a＜b”的逆命题是真命题 |
| B、命题“?x∈R，x2-x＞0”的否定是“?x∈R，x2-x＜0” |
| C、命题“p∨q”为真，则命题p，q都为真命题 |
| D、“x＞1”是“x＞2”的必要不充分条件 |
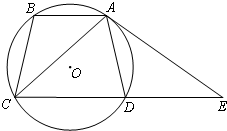如图，等腰梯形ABCD内接于⊙O，AB∥CD．过点A作⊙O的切线交CD的延长线于点E．求证：∠DAE=∠BAC．
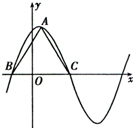函数f（x）=6cos2