题目内容
17.有两个命题:p:四边形的一组对边平行且相等q:四边形是矩形,则p是q的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
分析 利用平行四边形与矩形的定义及其关系即可得出.
解答 解:命题:p:四边形的一组对边平行且相等,可知此四边形为平行四边形,q:四边形是矩形,易知:矩形是平行四边形.
则p是q的必要不充分条件.
故选:B.
点评 本题考查了平行四边形与矩形的定义及其关系、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.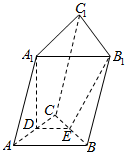 如图所示的三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于直线DE,则DE与AB的位置关系是( )
如图所示的三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于直线DE,则DE与AB的位置关系是( )
 如图所示的三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于直线DE,则DE与AB的位置关系是( )
如图所示的三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于直线DE,则DE与AB的位置关系是( )| A. | 异面 | B. | 平行 | C. | 相交 | D. | 以上均有可能 |
12.已知等差数列{an}的前n项和为Sn,若2a5+3a7+2a9=14,则S13等于( )
| A. | 26 | B. | 28 | C. | 52 | D. | 13 |
7.设集合M={-1,1},N=$\left\{{x\left|{\frac{1}{x}<2}\right.}\right\}$,则下列结论正确的是( )
| A. | N⊆M | B. | M⊆N | C. | M∩N=∅ | D. | M∪N=R |