题目内容
7．设集合M={-1，1}，N=$\left\{{x\left|{\frac{1}{x}＜2}\right.}\right\}$，则下列结论正确的是（ ）| A． | N⊆M | B． | M⊆N | C． | M∩N=∅ | D． | M∪N=R |
分析 由集合M={-1，1}，N=$\left\{{x\left|{\frac{1}{x}＜2}\right.}\right\}$={x|x＜0或x$＞\frac{1}{2}$}，逐一判断即可得答案．
解答 解：集合M={-1，1}，N=$\left\{{x\left|{\frac{1}{x}＜2}\right.}\right\}$={x|x＜0或x$＞\frac{1}{2}$}，
则M⊆N，故A错误；
M⊆N，故B正确；
M∩N={-1，1}，故C错误；
M∪N=N，故D错误．
故选：B．
点评 本题主要考查了集合的包含关系判断及应用，考查了分式不等式的解法，属于基础题．
练习册系列答案
相关题目
17．有两个命题：p：四边形的一组对边平行且相等q：四边形是矩形，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 即不充分也不必要条件 |
某汽车公司为了考查某4S店的服务态度，对到店维修保养的客户进行回访调查，每个用户在到此店维修或保养后可以对该店进行打分，最高分为10分．上个月公司对该4S店的100位到店维修保养的客户进行了调查，将打分的客户按所打分值分成以下几组：第一组[0，2），第二组[2，4），第三组[4，6），第四组[6，8），第五组[8，10]，得到频率分布直方图如图所示．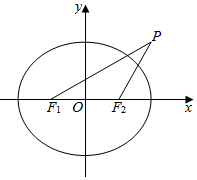
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的两个焦点为F1，F2，焦距为2，设点P（a，b）满足△PF1F2是等腰三角形．
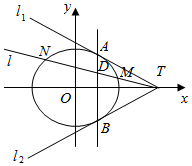已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1（a＞0）的两条切线方程y=±$\frac{1}{2}$（x-4），切点分别为A、B，且切线与x轴的交点为T．