题目内容
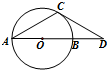 如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若CD=
如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若CD=| 3 |
考点:弦切角
专题:直线与圆
分析:由切割线定理得CD2=BD•DA,从而求出AB=3-1=2,由此能求出圆O的面积.
解答:
解:∵点D在圆O直径AB的延长线上,
过D作圆O的切线,切点为C.CD=
,BD=1,
∴CD2=BD•DA,
解得DA=
=
=3,
∴AB=3-1=2,
∴圆O的面积S=π•(
)2=π.
故答案为:π.
过D作圆O的切线,切点为C.CD=
| 3 |
∴CD2=BD•DA,
解得DA=
| CD2 |
| BD |
| 3 |
| 1 |
∴AB=3-1=2,
∴圆O的面积S=π•(
| 2 |
| 2 |
故答案为:π.
点评:本题考查圆的面积的求法,是基础题,解题时要认真审题,注意切割线定理的灵活运用.

练习册系列答案
相关题目
已知直线x=2及x=4与函数y=log2x图象的交点分别为A,B,与函数y=lgx图象的交点分别为C,D,则直线AB与CD( )
| A、平行 | B、垂直 | C、不确定 | D、相交 |
如图所示,不等式x(y-x-1)>0 表示的平面区域是( )
A、 |
B、 |
C、 |
D、 |
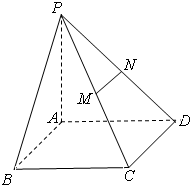 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是矩形,M、N分别是PC、PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是矩形,M、N分别是PC、PD的中点. 用4种不同的颜色给图中A、B、C、D四个区域涂色,要求相邻的区域涂色不同,则不同的涂色方法共有
用4种不同的颜色给图中A、B、C、D四个区域涂色,要求相邻的区域涂色不同,则不同的涂色方法共有