题目内容
函数y=
的定义域是（ ）
| ||
| x2+2x-3 |
| A、{x|x≥-3} |
| B、{x|x≥-3且x≠1} |
| C、{x|x≠-3且x≠1} |
| D、{x|x＞-3且x≠1} |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据二次根式的性质以及分母不为0，得不等式组，解出即可．
解答：
解：由题意得：
，
解得：x＞-3且x≠1，
故选：D．
|
解得：x＞-3且x≠1，
故选：D．
点评：本题考查了函数的定义域问题，考查了二次根式的性质，是一道基础题．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
设p：f（x）=x3-2x2-mx+1在（-∞，+∞）上单调递增；q：m＞
，则p是q的（ ）
| 4 |
| 3 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、以上都不对 |
已知复数z满足（3+i）z=10i（其中i是虚数单位，满足i2=-1），则复数z的共轭复数是（ ）
| A、-1+3i | B、1-3i |
| C、1+3i | D、-1-3i |
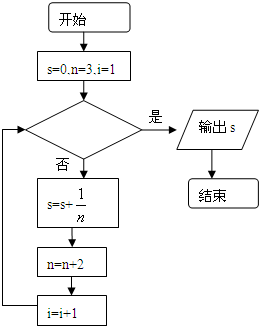
如图给出的是计算
+
+
+…+
的值的一个程序框图，其中判断框内应填入的条件是（ ）
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 21 |
| A、i＞10？ |
| B、i＜10？ |
| C、i＞20？ |
| D、i＜20？ |