题目内容
已知(1,1),(3,5)是等差数列{an}图象上的两点.
(1)求这个数列的通项公式;
(2)画出这个数列的图象;
(3)判断这个数列的单调性.
(1)求这个数列的通项公式;
(2)画出这个数列的图象;
(3)判断这个数列的单调性.
考点:数列的函数特性
专题:函数的性质及应用
分析:(1)利用等差数列的通项公式及其性质即可得出;
(2)图象是直线y=2x-1上一些等间隔的点;
(3)由于一次函数y=2x-1是单调递增,即可得出数列{an}单调性质.
(2)图象是直线y=2x-1上一些等间隔的点;
(3)由于一次函数y=2x-1是单调递增,即可得出数列{an}单调性质.
解答:
解:(1)∵(1,1),(3,5)是等差数列{an}图象上的两点.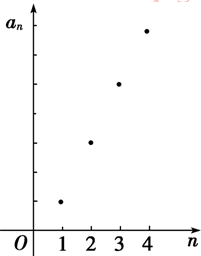
∴d=
=2,a1=1.
∴an=a1+(n-1)d=2n-1.
(2)图象是直线y=2x-1上一些等间隔的点(如图).
(3)由于一次函数y=2x-1是单调递增,因此数列{an}单调递增.

∴d=
| 5-1 |
| 3-1 |
∴an=a1+(n-1)d=2n-1.
(2)图象是直线y=2x-1上一些等间隔的点(如图).
(3)由于一次函数y=2x-1是单调递增,因此数列{an}单调递增.
点评:本题考查了等差数列的通项公式及其性质、等差数列与一次函数之间的关系,考查了类比能力,属于基础题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 如图所示,要建造一面靠墙的两间面积相同的矩形储备间,如果可供建造围墙的材料总长是30m,那么如何设计矩形的长和宽可使储备间的面积最大,并求这个最大面积.
如图所示,要建造一面靠墙的两间面积相同的矩形储备间,如果可供建造围墙的材料总长是30m,那么如何设计矩形的长和宽可使储备间的面积最大,并求这个最大面积.