题目内容
设函数y=f （x）的定义域为I，如果对于定义域I ，当 ，那么就说 f（x）在区间D上是增函数．
考点：函数的单调性及单调区间
专题：函数的性质及应用
分析：根据函数的增函数的定义即可得出答案．
解答：
解：由增函数的定义，可知，设函数y=f （x）的定义域为I，如果对于定义域I内某个区间D上的任意两个自变量x1，x2，x1＜x2时，都有f（x1）＜f（x2），那么就说 f（x）在区间D上是增函数．
故答案为：内某个区间D上的任意两个自变量x1，x2，x1＜x2时，都有f（x1）＜f（x2），
故答案为：内某个区间D上的任意两个自变量x1，x2，x1＜x2时，都有f（x1）＜f（x2），
点评：本题主要考查了函数的单调性的定义，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
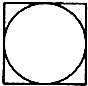如图是一个边长为1的正方形及其内切圆，现随机地向该正方形内投一粒黄豆（视为一点），则黄豆落入圆内的概率为函数f（x）=2x-1，x∈{-1，1}，则f（x）的值域为（ ）
| A、[-3，1） |
| B、（-3，1] |
| C、[-3，1] |
| D、{-3，1} |