题目内容
已知数列{an},{bn}满足a1=
,an+1=
,b1+2b2+22b3+…+2n-1bn=n(n∈N*).
(1)求数列{an}和{bn}的通项公式;
(2)设数列{
}的前n项和Tn,问是否存在正整数m、M,且M-n=3,使得m<Tn<M对一切n∈N*恒成立?若存在,求出m、M的值;若不存在,请说明理由.
| 2 |
| 3 |
| 2an |
| an+2 |
(1)求数列{an}和{bn}的通项公式;
(2)设数列{
| bn |
| an |
考点:数列递推式,数列的求和
专题:综合题,等差数列与等比数列
分析:(1)把数列递推式取倒数,整理得到数列{
}是等差数列,求出首项和公差,得到其通项公式,则数列
{an}的通项公式可求,再由b1+2b2+22b3+…+2n-1bn=n,取n=n-1得另一递推式,作差后可得数列{bn}的通项公式;
(2)把数列{an}和{bn}的通项公式代入
,利用错位相减法求前n项和Tn,由单调性结合放缩法证得答案.
| 1 |
| an |
{an}的通项公式可求,再由b1+2b2+22b3+…+2n-1bn=n,取n=n-1得另一递推式,作差后可得数列{bn}的通项公式;
(2)把数列{an}和{bn}的通项公式代入
| bn |
| an |
解答:
解:(1)由an+1=
,得
=
=
+
,即
-
=
.
∴数列{
}是首项为
=
,公差为
的等差数列.
∴
=
+(n-1)•
=
,即an=
.
∵b1+2b2+22b3+…+2n-1bn=n ①,
∴b1+2b2+22b3+…+2n-2bn-1=n-1 (n≥2)②.
①-②得2n-1bn=1,即bn=
(n≥2).
由①知,b1=1也满足上式,故bn=
;
(2)由(1)知,
=
,下面用“错位相减法”求Tn.
Tn=
+
+
+…+
③,
Tn=
+
+…+
+
④.
③-④得
Tn=
+
+
+…+
-
=2-
,
∴Tn=4-
<4.
又
>0,则数列{Tn}单调递增,故Tn≥T1=
>1,从而1<Tn<4.
因此,存在正整数m=1、M=4且M-m=3,使得m<Tm<M对一切n∈N*恒成立.
| 2an |
| an+2 |
| 1 |
| an+1 |
| an+2 |
| 2an |
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| 2 |
∴数列{
| 1 |
| an |
| 1 |
| a1 |
| 3 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| an |
| 3 |
| 2 |
| 1 |
| 2 |
| n+2 |
| 2 |
| 2 |
| n+2 |
∵b1+2b2+22b3+…+2n-1bn=n ①,
∴b1+2b2+22b3+…+2n-2bn-1=n-1 (n≥2)②.
①-②得2n-1bn=1,即bn=
| 1 |
| 2n-1 |
由①知,b1=1也满足上式,故bn=
| 1 |
| 2n-1 |
(2)由(1)知,
| bn |
| an |
| n+2 |
| 2n |
Tn=
| 3 |
| 2 |
| 4 |
| 22 |
| 5 |
| 23 |
| n+2 |
| 2n |
| 1 |
| 2 |
| 3 |
| 22 |
| 4 |
| 23 |
| n+1 |
| 2n |
| n+2 |
| 2n+1 |
③-④得
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| n+2 |
| 2n+1 |
| n+4 |
| 2n+1 |
∴Tn=4-
| n+4 |
| 2n |
又
| an |
| bn |
| 3 |
| 2 |
因此,存在正整数m=1、M=4且M-m=3,使得m<Tm<M对一切n∈N*恒成立.
点评:本题考查了数列递推式,考查了裂项相消法求数列的和,训练了放缩法证明数列不等式,是中档题.

练习册系列答案
相关题目
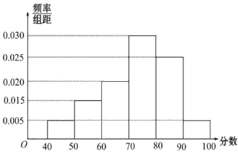 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.