Question

在等腰三角形ABC中，AB=AC，且D为AC中点，BD=

3

，则△ABC的面积最大值为

 

．

Answer 1

考点：正弦定理

专题：函数的性质及应用,不等式的解法及应用

分析：设AB=AC=2x，三角形的顶角θ，则由余弦定理求得cosθ的表达式，进而根据同角三角函数基本关系求得sinθ，最后根据三角形面积公式表示出三角形面积的表达式，根据一元二次函数的性质求得面积的最大值．

解答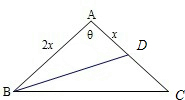： 解：设AB=AC=2x，AC=x．
设三角形的顶角θ，则由余弦定理得cosθ=

(2x)2+x2-3

4x2

=

5x2-3

4x2

，
∴sinθ=

1-cos2θ

=

1-( 5x2-3 4x2 )2

=

-9x4-9+30x2

4x2

=

1

4x2

-9(x2- 30 18 )2+9× 302-182 182

，
 根据公式三角形面积S=

1

2

absinθ=

1

2

×2x×2x×

1

4x2

-9(x2- 30 18 )2+9× 302-182 182

=

1

2

-9(x2- 30 18 )2+9× 302-182 182

，
∴当 x²=

30

18

时，三角形面积有最大值

1

2

9× 900-324 324

=2．
故答案为：2．

点评：本题主要考查函数最值的应用，根据条件设出变量，根据三角形的面积公式以及三角函数的关系是解决本题的关键，利用二次函数的性质即可求出函数的最值，考查学生的运算能力．运算量较大，属于中档题．