题目内容
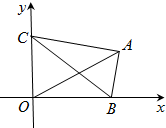 已知点G是△ABC的外心,
已知点G是△ABC的外心,| GA |
| GB |
| GC |
| GA |
| AB |
| AC |
| 0 |
| OA |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
考点:向量的加法及其几何意义
专题:平面向量及应用
分析:根据题意,得出:①G是BC的中点,△ABC是直角三角形,且斜边BC=2;
②点G的轨迹是以原点为圆心、1为半径的圆弧;
③OA经过BC的中点G时,|
|取得最大值为2|
|.
②点G的轨迹是以原点为圆心、1为半径的圆弧;
③OA经过BC的中点G时,|
| OA |
| GA |
解答:
解:∵点G是△ABC的外心,且2
+
+
=
,
∴点G是BC的中点,△ABC是直角三角形,∠BAC是直角;
又∵
,
,
是三个单位向量,
∴BC=2;
又∵△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,
∴点G的轨迹是以原点为圆心、1为半径的圆弧;
又∵|
|=1,
∴OA经过BC的中点G时,|
|取得最大值,最大值为2|
|=2.
故选:C.
| GA |
| AB |
| AC |
| 0 |
∴点G是BC的中点,△ABC是直角三角形,∠BAC是直角;
又∵
| GA |
| GB |
| GC |
∴BC=2;
又∵△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,
∴点G的轨迹是以原点为圆心、1为半径的圆弧;
又∵|
| GA |
∴OA经过BC的中点G时,|
| OA |
| GA |
故选:C.
点评:本题考查了平面向量的加法与减法的几何意义与应用问题,是基础题目.

练习册系列答案
相关题目
执行右边的程序框图,则输出的A是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=
的定义域为( )
| lg(1-2x) |
| A、(-∞,0] | ||
| B、(-∞,0) | ||
C、(0,
| ||
D、(-∞,
|
2sin15°cos15°=( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
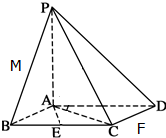 如图,已知四棱锥P-ABCD的底面为棱形,PA⊥底面ABCD,∠ABC=60°.E,F,M分别是BC,CD,PB的中点.
如图,已知四棱锥P-ABCD的底面为棱形,PA⊥底面ABCD,∠ABC=60°.E,F,M分别是BC,CD,PB的中点.