题目内容
16. 如图是一幅椭圆形彗星轨道图,长4cm,高2$\sqrt{3}$cm,已知O为椭圆的中心,A1,A2是长轴两端点,太阳位移椭圆的左焦点F处.
如图是一幅椭圆形彗星轨道图,长4cm,高2$\sqrt{3}$cm,已知O为椭圆的中心,A1,A2是长轴两端点,太阳位移椭圆的左焦点F处.(1)建立适当的坐标系,求椭圆的方程;
(2)求彗星运行到太阳正上方时两者在图上的距离.
分析 (1)如图所示,可设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意可得:2a=4,2$\sqrt{3}$=2b,解出即可得出.
(2)c=$\sqrt{{a}^{2}-{b}^{2}}$=1,可得F(1,0).把x=1代入椭圆标准方程解出即可得出.
解答  解:(1)如图所示,
解:(1)如图所示,
可设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
∵2a=4,2$\sqrt{3}$=2b,
解得a=2,b=$\sqrt{3}$.
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(2)c=$\sqrt{{a}^{2}-{b}^{2}}$=1,
∴F(1,0).
把x=1代入椭圆标准方程可得$\frac{1}{4}+\frac{{y}^{2}}{3}$=1,
解得y=±$\frac{3}{2}$.
∴彗星运行到太阳正上方时两者在图上的距离=$\frac{3}{2}$.
点评 本题考查了椭圆的标准方程及其应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.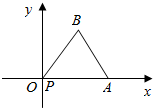 如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )
如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )
 如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )
如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )| A. | (-$\frac{37}{3}$,-9) | B. | (-∞,-$\frac{37}{3}$) | C. | (-$\frac{37}{3}$,-5) | D. | (-9,-5) |
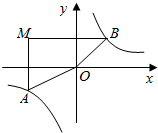 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.
如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.