题目内容
已知在锐角△ABC中,∠A=45°,a=2,c=
,求B和边b.
| 6 |
考点:正弦定理
专题:解三角形
分析:在锐角△ABC中,由正弦定理求得sinC=
,可得 C=60°,再由三角形内角和公式求得B,利用正弦定理求得b的值.
| ||
| 2 |
解答:
解:在锐角△ABC中,由正弦定理得:
=
,即
=
,
解得sinC=
,∴C=60°,∴B=180°-A-C=75°.
∴b=
sinB=
×
=
+1.
| a |
| sinA |
| c |
| sinC |
| 2 | ||||
|
| ||
| sinC |
解得sinC=
| ||
| 2 |
∴b=
| a |
| sinA |
| 2 | ||||
|
| ||||
| 4 |
| 3 |
点评:本题主要考查正弦定理、根据三角函数的值求角,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

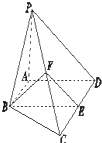 (文科)如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥AD,AB∥CD,AB⊥AD,CD=2AB,E和F分别是CD和PC的中点.求证:
(文科)如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥AD,AB∥CD,AB⊥AD,CD=2AB,E和F分别是CD和PC的中点.求证: