题目内容
求证:当x≥4时,
>lnx.
| x |
考点:利用导数研究函数的单调性,导数的运算
专题:导数的综合应用
分析:设函数f(x)=
-lnx(x>0),则f′(x)=
×
-
=
,令f'(x)=0,求出函数f(x)的单调区间,从而证明
>lnx成立.
| x |
| 1 |
| 2 |
| 1 | ||
|
| 1 |
| x |
| ||
| 2x |
| x |
解答:
证明:
>lnx等价于
-lnx>0
设函数f(x)=
-lnx(x>0),
则f′(x)=
×
-
=
,
令f'(x)=0,解得x=4,
当x>4时,f'(x)>0,
当x<4时,f'(x)<0,
∴当x=4,f(x)取得极小值,
∴f(x)的单调递增区间是[4,+∞),
f(x)≥f(4).
又当x=4时,f(x)=f(4)=2-ln4>0
∴x≥4时,f(x)>0,
即
-lnx>0,
∴
>lnx成立.
| x |
| x |
设函数f(x)=
| x |
则f′(x)=
| 1 |
| 2 |
| 1 | ||
|
| 1 |
| x |
| ||
| 2x |
令f'(x)=0,解得x=4,
当x>4时,f'(x)>0,
当x<4时,f'(x)<0,
∴当x=4,f(x)取得极小值,
∴f(x)的单调递增区间是[4,+∞),
f(x)≥f(4).
又当x=4时,f(x)=f(4)=2-ln4>0
∴x≥4时,f(x)>0,
即
| x |
∴
| x |
点评:本题考察了函数的单调性,导数的应用,不等式的证明,本题属于中档题.

练习册系列答案
相关题目

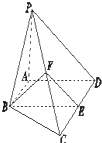 (文科)如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥AD,AB∥CD,AB⊥AD,CD=2AB,E和F分别是CD和PC的中点.求证:
(文科)如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥AD,AB∥CD,AB⊥AD,CD=2AB,E和F分别是CD和PC的中点.求证: