题目内容
1.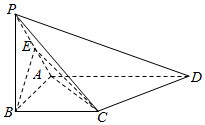 在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,E为PA的中点.
在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,E为PA的中点.(Ⅰ)求证:BE∥平面PCD;
(Ⅱ)若△PAC是边长为2的等边三角形,PB=$\sqrt{2}$,求三棱锥P-BEC的体积.
分析 (Ⅰ)取PD中点F,连结EF,FC,利用三角形中位线,得出EF∥AD,可得四边形EFCB为平行四边形,BE∥CF,从而BE∥平面PCD;
(Ⅱ)证明BC⊥平面PAB,PB⊥AB,转换底面根据锥体体积公式算出三棱锥P-BEC的体积.
解答 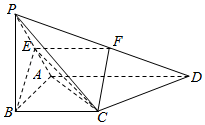 (Ⅰ)证明:∵△ABC与△ACD都是等腰直角三角形,∠ABC=∠ACD=90°,∴∠ACB=∠DAC=45°,$AC=\sqrt{2}BC,AD=\sqrt{2}AC$,
(Ⅰ)证明:∵△ABC与△ACD都是等腰直角三角形,∠ABC=∠ACD=90°,∴∠ACB=∠DAC=45°,$AC=\sqrt{2}BC,AD=\sqrt{2}AC$,
∴BC∥AD,$BC=\frac{1}{2}AD$,(2分)
取PD中点F,连结EF,FC,
∵E为PA的中点,
∴EF∥AD,$EF=\frac{1}{2}AD$,
∴EF∥BC,EF=BC,
∴四边形EFCB为平行四边形,
∴BE∥CF.(4分)
又BE?平面PCD,CF?平面PCD,
∴BE∥平面PCD.(6分)
(Ⅱ)解:∵$PB=\sqrt{2},BC=\sqrt{2},PC=2$,
∴PC2=PB2+BC2,
∴BC⊥PB.(7分)
又BC⊥AB,PB∩AB=B,
∴BC⊥平面PAB.(8分)
∵$PB=AB=\sqrt{2},PA=2$,
∴PA2=PB2+AB2,
∴PB⊥AB.(9分)
∴${S_{△PAB}}=\frac{1}{2}×\sqrt{2}×\sqrt{2}=1$.(10分)
∴VA-BEC=VC-PBE=$\frac{1}{3}•{S_{△PBE}}•CB$=$\frac{1}{3}×\frac{1}{2}{S_{△PAB}}•CB$=$\frac{1}{3}×1×\sqrt{2}$=$\frac{{\sqrt{2}}}{6}$.(12分)
点评 本题给出特殊的四棱锥,求证线面平行并求三棱锥的体积,着重考查了空间直线与平面平行的判定与性质和锥体体积公式等知识,考查空间想象能力、运算求解能力及推理论证能力,属于中档题.

| A. | 7 | B. | 14 | C. | 28 | D. | 56 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{3+3i}{2}$ | B. | $\frac{1+3i}{2}$ | C. | $\frac{1+i}{2}$ | D. | $\frac{3+i}{2}$ |
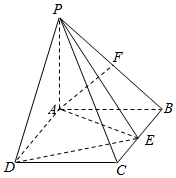 如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=1,AD=2,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=1,AD=2,点F是PB的中点,点E在边BC上移动.