题目内容

求双曲线3x2-y2=3的实半轴长和虚半轴长，焦点坐标，离心率，渐近线方程．
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：将双曲线方程化为标准方程，求得a，b，c，从而可求双曲线的几何性质．
解答： 解：把方程3x2-y2=3化为标准方程为x2-
y2
3
=1…（1分）
∴a=1，b=
3

∵c2=a2+b2=1+3=4，∴c=2…（2分）
实半轴长 a=1，虚半轴长b=
3
，焦点坐标F1（-2，0），F2（2，0）…（4分）
离心率e=
c
a
=2，渐近线方程y=±
3
x…（6分）
点评：本题以双曲线方程为载体，考查双曲线的标准方程，考查双曲线的几何性质，属于基础题．
练习册系列答案
相关题目
若
AB
•
BC
+
AB
2＞0，则△ABC为（　　）
A、锐角三角形
B、直角三角形
C、钝角三角形
D、以上答案均有可能
已知tanα=-
3
5
．
（Ⅰ）求sinαcosα-cos2α的值；
（Ⅱ）求
cos(3π+α)cos(
π
2
+α)cos(
11π
2
-α)
cos(π-α)sin(-π-α)sin(
9
2
π+α)
的值．
已知
a
=（sinωx，
3
sinωx），
b
=（sinωx，cosωx）（ω＞0），函数f（x）=
a
•
b
-
1
2
，且f（x）的最小正周期为π．
（Ⅰ）求ω的值；
（Ⅱ）求函数f（x）的单调递增区间．
对10个接受心脏搭桥手术的病人和10个接受血管清障手术的病人进行了3年的跟踪研究，调查他们是否又发作过心脏病，调查结果如下表所示：
又发作过心脏病未发作过心脏病合计
心脏搭桥手术3710
血管清障手术5510
合计81220
试根据上述数据计算X2．
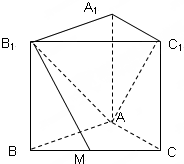如图，正三棱柱ABC-A1B1C1中，点M是BC的中点，AB=2，BB1=
3

（Ⅰ）求直线B1M与平面AB1C1所成角的正弦；
（Ⅱ）求异面直线B1M与AC的距离．
已知函数f（x）=x4+ax3+2x2+b（x∈R），其中a，b∈R．
（Ⅰ）当a∈[-2，2]时，求函数f（x）的极值点；
（Ⅱ）若对于任意的a∈[-2，2]，不等式f（x）≤1在[-1，1]上恒成立，求b的取值范围．
两颗正四面体的玩具，其四个面上分别标有数字1，2，3，4，下面做投掷这两颗正四面体玩具的实验：用（x，y）表示结果，其中x表示第1颗正四面体玩具出现的点数，y表示第2颗正四面体出现的点数．
（1）求事件“出现点数之和小于5的概率；
（2）求事件“出现点数相等”的概率．
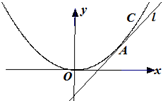如图，直线l：y=x+b与曲线C：x2=4y相切于点A．
（Ⅰ）求实数b的值；
（Ⅱ）求由曲线C与直线l及x=0围成的图形的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网