题目内容
(1)已知椭圆的短轴与焦距相等,求椭圆的离心率;
(2)已知正方形ABCD,求以A、B为焦点,且过C、D两点的椭圆的离心率.
(2)已知正方形ABCD,求以A、B为焦点,且过C、D两点的椭圆的离心率.
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)由于椭圆的短轴与焦距相等,即2c=2b,即可求椭圆的离心率;
(2)由“以A、B为焦点”可求得c,再由“过C、D两点”结合椭圆的定义可知|AC|+|BC|=2a,可求a,再由离心率公式求得其离心率.
(2)由“以A、B为焦点”可求得c,再由“过C、D两点”结合椭圆的定义可知|AC|+|BC|=2a,可求a,再由离心率公式求得其离心率.
解答:
解:(1)由于椭圆的短轴与焦距相等,即2c=2b,
∴c=b,∴a=
=
c,
∴e=
=
;
(2)设正方形边长为1,则AB=2c=1,
∴c=
.
∵|AC|+|BC|=1+
=2a,
∴a=
.
∴e=
=
-1.
∴c=b,∴a=
| b2+c2 |
| 2 |
∴e=
| c |
| a |
| ||
| 2 |
(2)设正方形边长为1,则AB=2c=1,
∴c=
| 1 |
| 2 |
∵|AC|+|BC|=1+
| 2 |
∴a=
| ||
| 2 |
∴e=
| c |
| a |
| 2 |
点评:本题考查椭圆的标准方程,以及简单性质的应用,题目灵活新颖,转化巧妙,是一道好题.

练习册系列答案
相关题目
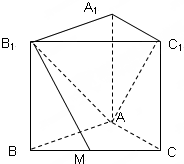 如图,正三棱柱ABC-A1B1C1中,点M是BC的中点,AB=2,BB1=
如图,正三棱柱ABC-A1B1C1中,点M是BC的中点,AB=2,BB1=