题目内容
19.已知三次函数$f(x)=\frac{1}{3}{x^3}-({4m-1}){x^2}+({15{m^2}-2m-7})x+2$在x∈(-∞,+∞)是增函数,则m的取值范围是( )| A. | m<2或m>4 | B. | -4<m<-2 | C. | 2<m<4 | D. | 以上皆不正确 |
分析 求出函数的导数,通过△=4(4m-1)2-4(15m2-2m-7)≤0,解出即可.
解答 解:∵f(x)=$\frac{1}{3}$x3-(4m-1)x2+(15m2-2m-7)x+2,
∴f′(x)=x2-2(4m-1)x+(15m2-2m-7)>0,
∴△=4(4m-1)2-4(15m2-2m-7)<0,
解得:2<m<4,
故选:C.
点评 本题考察了函数的单调性,导数的应用,是一道基础题.

练习册系列答案
相关题目
14.设甲、乙两楼相距10m,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则甲、乙两楼的高分别是( )
| A. | $\frac{10\sqrt{3}}{3}$m,$\frac{40}{3}$$\sqrt{3}$ m | B. | 10$\sqrt{3}$ m,20$\sqrt{3}$ m | C. | 10($\sqrt{3}$-$\sqrt{2}$) m,20$\sqrt{3}$ m | D. | 10$\sqrt{3}$ m,$\frac{40}{3}$$\sqrt{3}$ m |
8.已知直线l:x-$\sqrt{3}$y+6=0与圆x2+y2=12交于A,B两点,过A,B分别作l的垂线与x轴交于C,D两点,则|CD|=( )
| A. | $2\sqrt{3}$ | B. | 4 | C. | $4\sqrt{3}$ | D. | 6 |
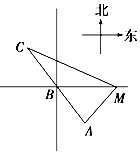 如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于2km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,则塔M到直路ABC的最短距离为$\frac{14+10\sqrt{3}}{13}$.
如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于2km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,则塔M到直路ABC的最短距离为$\frac{14+10\sqrt{3}}{13}$.