题目内容
如图，设椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
（Ⅰ）已知直线l的斜率为k，用a，b，k表示点P的坐标；
（Ⅱ）若过原点O的直线l1与l垂直，证明：点P到直线l1的距离的最大值为a-b．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析：（Ⅰ）设直线l的方程为y=kx+m（k＜0），由
，消去y得（b2+a2k2）x2+2a2kmx+a2m2-a2b2=0，利用△=0，可求得在第一象限中点P的坐标；
（Ⅱ）由于直线l1过原点O且与直线l垂直，设直线l1的方程为x+ky=0，利用点到直线间的距离公式，可求得点P到直线l1的距离d=
，整理即可证得点P到直线l1的距离的最大值为a-b．．
|
（Ⅱ）由于直线l1过原点O且与直线l垂直，设直线l1的方程为x+ky=0，利用点到直线间的距离公式，可求得点P到直线l1的距离d=
|
| ||||||||
|
解答：
解：（Ⅰ）设直线l的方程为y=kx+m（k＜0），由
，消去y得
（b2+a2k2）x2+2a2kmx+a2m2-a2b2=0．
由于直线l与椭圆C只有一个公共点P，故△=0，即b2-m2+a2k2=0，解得点P的坐标为
（-
，
），
又点P在第一象限，故点P的坐标为P（
，
）．
（Ⅱ）由于直线l1过原点O且与直线l垂直，故直线l1的方程为x+ky=0，所以点P到直线l1的距离
d=
，
整理得：d=
，
因为a2k2+
≥2ab，所以
≤
=a-b，当且仅当k2=
时等号成立．
所以，点P到直线l1的距离的最大值为a-b．
|
（b2+a2k2）x2+2a2kmx+a2m2-a2b2=0．
由于直线l与椭圆C只有一个公共点P，故△=0，即b2-m2+a2k2=0，解得点P的坐标为
（-
| a2km |
| b2+a2k2 |
| b2m |
| b2+a2k2 |
又点P在第一象限，故点P的坐标为P（
| -a2k | ||
|
| b2 | ||
|
（Ⅱ）由于直线l1过原点O且与直线l垂直，故直线l1的方程为x+ky=0，所以点P到直线l1的距离
d=
|
| ||||||||
|
整理得：d=
| a2-b2 | ||||
|
因为a2k2+
| b2 |
| k2 |
| a2-b2 | ||||
|
| a2-b2 | ||
|
| b |
| a |
所以，点P到直线l1的距离的最大值为a-b．
点评：本题主要考查椭圆的几何性质、点到直线间的距离、直线与椭圆的位置关系等基础知识，同时考查解析几何的基本思想方法、基本不等式应用等综合解题能力．
练习册系列答案
相关题目
已知集合A={y丨y=x2}，B={x丨
＜0}，求A∩B=（ ）
| x+1 |
| x-2 |
| A、[0，+∞） |
| B、（-1，2） |
| C、[0，2） |
| D、（-1，0] |
已知全集U={x∈N*丨-1≤x≤7}，集合M={2，4，6}，P={3，4，5}，那么集合∁U（M∪P）是（ ）
| A、{-1，0，1，7} |
| B、{1，7} |
| C、{1，3，7} |
| D、∅ |
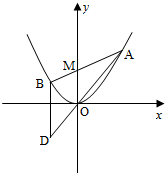如图，已知抛物线C：x2=4y，过点M（0，2）任作一直线与C相交于A，B两点，过点B作y轴的平行线与直线AO相交于点D（O为坐标原点）．