题目内容
 函数f(x)=6cos2
函数f(x)=6cos2| ωx |
| 2 |
| 3 |
(1)若x∈[0,1],求函数f(x)的值域;
(2)若f(x0)=
8
| ||
| 5 |
| 10 |
| 3 |
| 2 |
| 3 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的单调性
专题:三角函数的求值,三角函数的图像与性质
分析:(1)化简可得f(x)=2
sin(ωx+
),由已知可得周期,进而可得ω,可得函数的解析式,由x的范围可得;
(2)由题意直接可求f(x0)+1的值.
| 3 |
| π |
| 3 |
(2)由题意直接可求f(x0)+1的值.
解答:
解:(1)由已知得f(x)=6cos2
+
sinωx-3=3cosωx+
sinωx=2
sin(ωx+
)
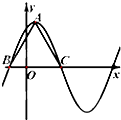
又△ABC为正三角形,且高为2
,可得BC=4.
∴函数f(x)的最小正周期为8,即
=8,
解得ω=
,∴f(x)=2
sin(
x+
),
∵x∈[0,1],∴
x+
∈[
,
],
∴sin(
x+
)∈[
,1]
∴f(x)∈[3,2
],
∴函数f(x)的值域为:[3,2
];
(2)∵f(x0)=
,
∴f(x0)+1=
+1.
| ωx |
| 2 |
| 3 |
| 3 |
| 3 |
| π |
| 3 |
又△ABC为正三角形,且高为2
| 3 |
∴函数f(x)的最小正周期为8,即
| 2π |
| ω |
解得ω=
| π |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 3 |
∵x∈[0,1],∴
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| 7π |
| 12 |
∴sin(
| π |
| 4 |
| π |
| 3 |
| ||
| 2 |
∴f(x)∈[3,2
| 3 |
∴函数f(x)的值域为:[3,2
| 3 |
(2)∵f(x0)=
8
| ||
| 5 |
∴f(x0)+1=
8
| ||
| 5 |
点评:本题考查两角和与差的三角函数公式,涉及同角三角函数的基本关系和三角函数的值域,属于基本知识的考查.

练习册系列答案
相关题目
设x+3y=2,则函数z=3x+27y的最小值是( )
| A、12 | B、27 | C、6 | D、30 |
 如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本为S元.
如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本为S元.