题目内容
2.已知a>0,x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤4}\\{y≥a(x-4)}\end{array}\right.$,若z=2x+y的最小值是-1,则a=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 1 |
分析 作出不等式对应的平面区域,利用线性规划的知识,通过平移先确定z的最优解,然后确定a的值即可.
解答 解:先根据约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤4}\\{y≥a(x-4)}\end{array}\right.$画出可行域,如图示:若z=2x+y的最小值是-1,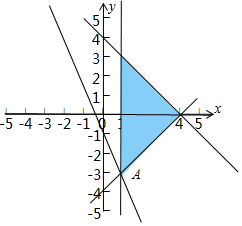 ,
,
z=2x+y,
将最小值转化为y轴上的截距的最小值,
当直线z=2x+y经过点A时,z最小,
由 $\left\{\begin{array}{l}{x=1}\\{2x+y=-1}\end{array}\right.$得:B(1,-3),代入直线y=a(x-4)得,a=1;
故选:D.
点评 本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
12.若△ABC的内角A,B,C所对的边分别是a、b、c,已知2bsin2A=asinB,且b=2,c=3,则a等于( )
| A. | $\sqrt{6}$ | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 4 |
13.下列四组函数,表示同一函数的是( )
| A. | $f(x)=\sqrt{x^2},g(x)=x$ | B. | $f(x)=\frac{{{x^2}-1}}{x-1},g(x)=x+1$ | ||
| C. | $f(x)=\sqrt{{x^2}-4},g(x)=\sqrt{x+2}\sqrt{x-2}$ | D. | $f(x)=lg2-lgx,g(x)=lg\frac{2}{x}$ |
11.命题“?x∈R,2x>0”的否定是( )
| A. | ?x∈R,2x>0 | B. | ?x∈R,2x≤0 | C. | ?x∈R,2x<0 | D. | ?x∈R,2x≤0 |