题目内容
已知不等式(
-m)•ln(
)≥0对任意正整数n恒成立,则实数m的取值范围是 .
| 20 |
| n |
| m |
| n |
考点:函数恒成立问题
专题:计算题,不等式的解法及应用
分析:由题意,
-m≥0,且ln(
)≥0或
-m≤0,且ln(
)≤0,化简可得n≤m≤
,或
≤m≤n,根据n为正整数,可得n=4或5,即可确定实数m的取值范围.
| 20 |
| n |
| m |
| n |
| 20 |
| n |
| m |
| n |
| 20 |
| n |
| 20 |
| n |
解答:
解:由题意,
-m≥0,且ln(
)≥0或
-m≤0,且ln(
)≤0,
∴m≤
,且
≥1或m≥
,且0<
≤1,
∴n≤m≤
,或
≤m≤n,
∵n为正整数,
∴n=4或5,
∴4≤m≤5,
故答案为:[4,5].
| 20 |
| n |
| m |
| n |
| 20 |
| n |
| m |
| n |
∴m≤
| 20 |
| n |
| m |
| n |
| 20 |
| n |
| m |
| n |
∴n≤m≤
| 20 |
| n |
| 20 |
| n |
∵n为正整数,
∴n=4或5,
∴4≤m≤5,
故答案为:[4,5].
点评:本题考查恒成立问题,考查学生分析解决问题的能力,由题意,
-m≥0,且ln(
)≥0或
-m≤0,且ln(
)≤0,是解题的关键.
| 20 |
| n |
| m |
| n |
| 20 |
| n |
| m |
| n |

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
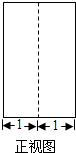 三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形,其正视图(如图所示)的面积为8,则该三棱柱左视图的面积为( )
三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形,其正视图(如图所示)的面积为8,则该三棱柱左视图的面积为( )A、2
| ||||
B、
| ||||
C、4
| ||||
D、8
|
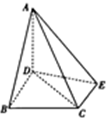 在三棱椎A-BCD中,AB=BC=4,AD=BD=CD=2
在三棱椎A-BCD中,AB=BC=4,AD=BD=CD=2