题目内容

函数y=
x
x-1
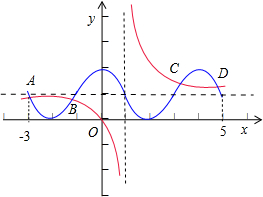
图象与函数y=2cos2
π
4
x（-3≤x≤5）图象所有交点的纵坐标之和
 
．
考点：二倍角的余弦
专题：三角函数的求值
分析：所以它的图象关于点（1，1）中心对称，再由正弦函数的对称中心公式，可得函数y=cos
π
2
x+1的图象的一个对称中心也是点（1，1），故交点个数为偶数，且每一对对称点的横坐标之和为2．由此不难得到正确答案
解答： 解：∵函数y=
x
x-1
=
x-1+1
x-1
=1+
1
x-1
 的图象关于点（1，1）对称，
函数y=2cos2
π
4
x=cos
π
2
x+1的图象也关于点（1，1）对称，周期为
2π
π
2
=4，
在区间[-3，5]上，正好包含函数y=cos
π
2
x+1的2个周期，
2个图象的交点有4个，这4个交点可分成2对，每一对都关于点（1，1）对称，
故它们的纵坐标之和为4，
故答案为：4．
点评：发现两个图象公共的对称中心是解决本题的入口，讨论函数y=cos
π
2
x+1的单调性找出区间[-3，5]上的交点个数是本题的难点所在，属于中档题．
练习册系列答案
相关题目
在△ABC中，
AE
=2
EB
，
BC
=2
BD
，则
DE
=（　　）
A、-
1
3
AB
-
1
2
BC
B、
1
3
AB
-
1
2
BC
C、
1
2
AB
-
1
3
BC
D、-
1
3
AB
+
1
2
BC
正项数列{an}满足f（an）=
2
2-an
（an≠2），且{an}的前n项和Sn=
1
4
[3-
2
f(an)
]2．
（Ⅰ）求证：{an}是等差数列；
（Ⅱ）若bn=
an
2n
，求数列{bn}的前n项和Tn．
在△ABC中，a，b，c分别为内角A，B，C的对边，2asinA=（2b+c）sinB+（2c+b）sinC．
（Ⅰ）求角A的大小
（Ⅱ）求函数f（x）=cos2x-4cosAsinx（x∈R）的值域．
给出以下几个命题：
①由曲线y=x2与直线y=2x围成的封闭区域的面积为
4
3
．
②已知点A是定圆C上的一个定点，线段AB为圆的动弦，若
OP
=
1
2
（
OA
+
OB
），O为坐标原点，则动点P的轨迹为圆；
③把5本不同的书分给4个人，每人至少1本，则不同的分法种数为
A
4
5
•
A
1
4
=480种．
④若直线l∥平面α，直线l⊥直线m，直线l?平面β，则β⊥α．
其中，正确的命题有
 
．（将所有正确命题的序号都填在横线上）
某次数学考试中有三道选做题，分别为选做题1、2、3．规定每位考生必须且只须在其中选做一题．甲、乙、丙三名考生选做这一题中任意一题的可能性均为
1
3
，每位学生对每题的选择是相互独立的，各学生的选择相互之间没有影响．
（1）求这三个人选做的是同一道题的概率：
（2）设ξ为三个人中做选做题l的人数，求ξ的分布列与均值．
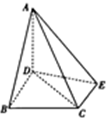在三棱椎A-BCD中，AB=BC=4，AD=BD=CD=2
2
，在底面BCD内作CE⊥CD，且CE=
2
．
（1）求证：CE∥平面ABD；
（2）如果二面角A-BD-C的大小为90°，求二面角B-AC-E的余弦值．
已知
a
=（sinα，1），
b
=（cosα，2），α∈（0，
π
4
）．
（1）若
a
•
b
=
17
8
，求sinα-cosα的值；
（2）若
a
∥
b
，又β为锐角，且tanβ=
1
3
，求α+β的值．
设f（x）=-cosx-sinx，f′（x）是其导函数．若命题“?x∈[
π
2
，π]，f′（x）＜a”是真命题，则实数a的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网