题目内容
已知复数z=a+bi(a,b∈R),若
=
-3aki(k∈R),求:
(1)2a+b的值;
(2)|z-i|+|z+i|的最小值.
| z |
| 2+4i |
| k |
(1)2a+b的值;
(2)|z-i|+|z+i|的最小值.
考点:复数求模
专题:数系的扩充和复数
分析:(1)利用复数的运算法则、共轭复数的定义、复数相等即可得出.
(2)利用复数的几何意义、轴对称即可得出.
(2)利用复数的几何意义、轴对称即可得出.
解答:
解:(1)∵复数z=a+bi(a,b∈R),
=
-3aki(k∈R),
∴a-bi=
+(
-3ak)i,
∴a=
,-b=
-3ak,
解得a=
,b=6-
.
∴2a+b=
+6-
=6.
(2)∵2a+b=6,
∴b=-2a+6,
设点P(0,1)关于直线y=-2x+6的对称点为P′(x,y),
则
,解得
,
∴P′(4,3).
Q(0,-1).
|z-i|+|z+i|≥|P′Q|=
=4
,
其最小值为4
.
| z |
| 2+4i |
| k |
∴a-bi=
| 2 |
| k |
| 4 |
| k |
∴a=
| 2 |
| k |
| 4 |
| k |
解得a=
| 2 |
| k |
| 4 |
| k |
∴2a+b=
| 4 |
| k |
| 4 |
| k |
(2)∵2a+b=6,
∴b=-2a+6,
设点P(0,1)关于直线y=-2x+6的对称点为P′(x,y),
则
|
|
∴P′(4,3).
Q(0,-1).
|z-i|+|z+i|≥|P′Q|=
| 42+42 |
| 2 |
其最小值为4
| 2 |
点评:本题考查了复数的运算法则、共轭复数的定义、复数相等、复数的几何意义、轴对称,考查了计算能力,属于中档题.

练习册系列答案
相关题目
直线方程3x+2y-6=0的斜率为k,在y轴上的截距为b,则有( )
A、k=-
| ||
B、k=-
| ||
C、k=-
| ||
D、k=-
|
已知角α终边上有一点P(3,-4),则sinα的值是( )
A、-
| ||
B、
| ||
C、±
| ||
D、±
|
已知函数f(x)=sin(ωx+
)(ω>0)的一条对称轴是x=
,则函数f(x)的最小正周期不可能是( )
| π |
| 4 |
| π |
| 8 |
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
下面不等式成立的是( )
| A、1.72.5>1.73 |
| B、log0.23<log0.25 |
| C、1.73.1<0.93.1 |
| D、log30.2<log0.20.3 |
复数(1-
)(1+i)=( )
| 1 |
| i |
| A、-2 | B、-2i | C、2 | D、2i |
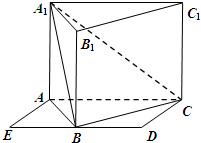 如图,侧棱垂直于底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AA1=4,∠E=60°,点B为DE中点,AB⊥BC.
如图,侧棱垂直于底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AA1=4,∠E=60°,点B为DE中点,AB⊥BC.