Question

3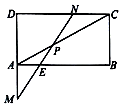．如图，矩形ABCD，AB=2，AD=1，P是对角线AC上一点，$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$，过P的直线分别交DA的延长线，AB，DC于M，E，N，若$\overrightarrow{DM}=m\overrightarrow{DA}，\overrightarrow{DN}=n\overrightarrow{DC}$，则2m+3n的最小值是（　　）

• A． $\frac{6}{5}$
• B． $\frac{12}{5}$
• C． $\frac{24}{5}$
• D． $\frac{48}{5}$

Answer 1

分析 梅涅劳斯定理，$\frac{CN}{DN}×\frac{DM}{AM}×\frac{AP}{PC}=1$，$\overrightarrow{DM}=m\overrightarrow{DA}，\overrightarrow{DN}=n\overrightarrow{DC}$，$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$，求出m，n的关系，即可利用基本不等式求解2m+3n的最小值．

解答 解：矩形ABCD，AB=2，AD=1，P是对角线AC上一点，$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$，
可得：$AP=\frac{2}{5}\sqrt{5}$，$PC=\frac{3}{5}\sqrt{5}$，
由梅涅劳斯定理，$\frac{CN}{DN}×\frac{DM}{AM}×\frac{AP}{PC}=1$，$\overrightarrow{DM}=m\overrightarrow{DA}，\overrightarrow{DN}=n\overrightarrow{DC}$，
可得：$\frac{2-2n}{2n}×\frac{m}{m-1}×\frac{\frac{2}{5}\sqrt{5}}{\frac{3}{5}\sqrt{5}}=1$，即$（\frac{1}{n}-1）×\frac{m}{m-1}×\frac{2}{3}=1$，
⇒2m+3n=5mn，
2m+3n≥$2\sqrt{6mn}$，
解的：mn$≥\frac{24}{25}$．
当且仅当2m=3n时取等号，
∴2m+3n=5mn≥$\frac{24}{5}$
故选C．

点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意平面向量加法法则的合理运用