题目内容
8．设点P是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）上的一点，F1、F2分别是双曲线的左、右焦点，已知PF1⊥PF2，且|PF1|=2|PF2|，则双曲线的一条渐近线方程是（ ）| A． | $y=\sqrt{2}x$ | B． | $y=\sqrt{3}x$ | C． | y=2x | D． | y=4x |
分析 根据双曲线的定义可知|PF1|-|PF2|=2a，进而根据|PF1|=2|PF2|，分别求得|PF2|和|PF1|，进而根据勾股定理建立等式求得a和c的关系，然后求解渐近线方程．
解答 解：由双曲线的定义可得|PF1|-|PF2|=2a，
又|PF1|=2|PF2|，
得|PF2|=2a，|PF1|=4a；
在RT△PF1F2中，|F1F2|2=|PF1|2+|PF2|2，
∴4c2=16a2+4a2，即c2=5a2，
则b2=4a2．即b=2a，
双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1一条渐近线方程：y=2x；
故选：C．
点评 本题主要考查了双曲线的渐近线的求法．考查了学生对双曲线定义和基本知识的掌握．
练习册系列答案
相关题目
16．已知直线2x-y-3=0的倾斜角为θ，则sin2θ的值是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{5}$ | D． | $\frac{2}{5}$ |
3．
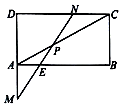如图，矩形ABCD，AB=2，AD=1，P是对角线AC上一点，$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$，过P的直线分别交DA的延长线，AB，DC于M，E，N，若$\overrightarrow{DM}=m\overrightarrow{DA}，\overrightarrow{DN}=n\overrightarrow{DC}$，则2m+3n的最小值是（ ）
如图，矩形ABCD，AB=2，AD=1，P是对角线AC上一点，$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$，过P的直线分别交DA的延长线，AB，DC于M，E，N，若$\overrightarrow{DM}=m\overrightarrow{DA}，\overrightarrow{DN}=n\overrightarrow{DC}$，则2m+3n的最小值是（ ）| A． | $\frac{6}{5}$ | B． | $\frac{12}{5}$ | C． | $\frac{24}{5}$ | D． | $\frac{48}{5}$ |