题目内容
13．已知集合A={a，b}，B={a，b，c，d，e}，满足条件A⊆M⊆B的集合M的个数为8．分析 列举出满足条件的集合M，从而判断其个数即可．
解答 解：∵A={a，b}，B={a，b，c，d，e}，A⊆M⊆B，
∴M={a，b}，{a，b，c}，{a，b，d}，{a，b，e}，
{a，b，c，d}，{a，b，c，e}，{a，b，d，e}，{a，b，c，d，e}，
共8个，
故答案为：8．
点评 本题考查了集合的子集和真子集的定义，是一道基础题．
练习册系列答案
相关题目
18．已知数列{an}的前n项和为Sn，Sn=4n2+2n，则此数列的通项公式为（ ）
| A． | an=2n-2 | B． | an=8n-2 | C． | an=2n-1 | D． | an=n2-n |
1．已知f（x）=$\left\{{\begin{array}{l}{{a^x}，x＞1}\\{（4-\frac{a}{2}）x+2，x≤1}\end{array}}$是R上的增函数，则实数a的取值范围（ ）
| A． | [4，8 ） | B． | （4，8） | C． | （1，8） | D． | （1，+∞） |
2．已知集合A={x|-3≤x＜2}，B={x|x≥m}，且A⊆B，则实数m的取值范围是（ ）
| A． | {m|m≥-3} | B． | {m|m≤-3} | C． | {m|m≤2} | D． | {m|m≥2} |
3．
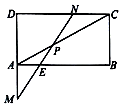如图，矩形ABCD，AB=2，AD=1，P是对角线AC上一点，$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$，过P的直线分别交DA的延长线，AB，DC于M，E，N，若$\overrightarrow{DM}=m\overrightarrow{DA}，\overrightarrow{DN}=n\overrightarrow{DC}$，则2m+3n的最小值是（ ）
如图，矩形ABCD，AB=2，AD=1，P是对角线AC上一点，$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$，过P的直线分别交DA的延长线，AB，DC于M，E，N，若$\overrightarrow{DM}=m\overrightarrow{DA}，\overrightarrow{DN}=n\overrightarrow{DC}$，则2m+3n的最小值是（ ）| A． | $\frac{6}{5}$ | B． | $\frac{12}{5}$ | C． | $\frac{24}{5}$ | D． | $\frac{48}{5}$ |