题目内容
13.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0),F(c,0)为椭圆右焦点,A为椭圆左顶点,且b2=ac,P为椭圆上不同于A的点,则使$\overrightarrow{PA}$•$\overrightarrow{PF}$=0的点P的个数为( )| A. | 4 | B. | 3 | C. | 2 | D. | 0 |
分析 根据椭圆a,b,c,可得F,A的坐标,设P(x,y),根据$\overrightarrow{PA}$•$\overrightarrow{PF}$=0和点P在椭圆上,解得即可得到交点个数.
解答 解:由题意可知:椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0),焦点在x轴上,设P(x,y),
则F(c,0),A(-a,0),
由$\overrightarrow{PA}$=(-a-x,-y),$\overrightarrow{PF}$=(c-x,-y),
由$\overrightarrow{PA}$•$\overrightarrow{PF}$=0,则(-a-x)(c-x)+y2=0,
-ac+(a-c)x+x2+y2=0,
由P在椭圆上,y2=b2(1-$\frac{{x}^{2}}{{a}^{2}}$),
∴-ac+(a-c)x+x2+b2(1-$\frac{{x}^{2}}{{a}^{2}}$)=0,
由b2=ac,
∴(1-$\frac{c}{a}$)x2+(a-c)x=0
解得:x=0,x=-a,
∴当x=0时,y=±b,
当x=-a时,y=0,
∵P为椭圆上不同于A的点,
∴P点的坐标为(0,b)或(0,-b),
∴使$\overrightarrow{PA}$•$\overrightarrow{PF}$=0的点P的个数为2个,
故选:C.
点评 本题考查椭圆的方程和性质,以及向量的数量积公式,考查了学生的运算能力,属于中档题.

练习册系列答案
相关题目
3.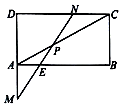 如图,矩形ABCD,AB=2,AD=1,P是对角线AC上一点,$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$,过P的直线分别交DA的延长线,AB,DC于M,E,N,若$\overrightarrow{DM}=m\overrightarrow{DA},\overrightarrow{DN}=n\overrightarrow{DC}$,则2m+3n的最小值是( )
如图,矩形ABCD,AB=2,AD=1,P是对角线AC上一点,$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$,过P的直线分别交DA的延长线,AB,DC于M,E,N,若$\overrightarrow{DM}=m\overrightarrow{DA},\overrightarrow{DN}=n\overrightarrow{DC}$,则2m+3n的最小值是( )
 如图,矩形ABCD,AB=2,AD=1,P是对角线AC上一点,$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$,过P的直线分别交DA的延长线,AB,DC于M,E,N,若$\overrightarrow{DM}=m\overrightarrow{DA},\overrightarrow{DN}=n\overrightarrow{DC}$,则2m+3n的最小值是( )
如图,矩形ABCD,AB=2,AD=1,P是对角线AC上一点,$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$,过P的直线分别交DA的延长线,AB,DC于M,E,N,若$\overrightarrow{DM}=m\overrightarrow{DA},\overrightarrow{DN}=n\overrightarrow{DC}$,则2m+3n的最小值是( )| A. | $\frac{6}{5}$ | B. | $\frac{12}{5}$ | C. | $\frac{24}{5}$ | D. | $\frac{48}{5}$ |
1.$({x+\frac{a}{x}}){({2x-\frac{1}{x}})^5}$展开式中,各项系数之和为3,则展开式中的常数项为( )
| A. | -120 | B. | -80 | C. | 80 | D. | 120 |
5.已知命题$p:x≠\frac{π}{6}+2kπ,k∈Z$;命题$q:sinx≠\frac{1}{2}$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.已知函数f(x)=ax-1(a>0,且a≠1),当x∈(0,+∞)时,f(x)>0,且函数g(x)=f(x+1)-4的图象不过第二象限,则a的取值范围是( )
| A. | (1,+∞) | B. | $(\frac{1}{2},1)$ | C. | (1,3] | D. | (1,5] |