题目内容
18．正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的体积为$\frac{243}{16}π$．分析 正四棱锥P-ABCD的五个顶点在同一球面上，则其外接球的球心在它的高PO1上，记为O，如图．求出AO1，OO1，解出球的半径，求出球的体积．
解答 
解：正四棱锥P-ABCD的外接球的球心在它的高PO1上，
记为O，PO=AO=R，PO1=4，OO1=4-R，
在Rt△AO1O中，AO1=$\sqrt{2}$，由勾股定理R2=2+（4-R）2得R=$\frac{9}{4}$，
∴球的体积为$\frac{243}{16}π$．
故答案为：$\frac{243}{16}π$．
点评 本题考查球的表面积，球的内接体问题，解答关键是确定出球心的位置，利用直角三角形列方程式求解球的半径．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
6．已知△ABC中，角A，B，C所对的边分别为a，b，c，D是BC的中点，且AD=$\sqrt{10}$，若S△ABC=4，b＞c，且$\frac{b-csinA}{a}$=cosC，则B的值为（ ）
| A． | 60° | B． | 120° | C． | 45° | D． | 90° |
3．
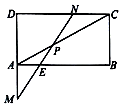如图，矩形ABCD，AB=2，AD=1，P是对角线AC上一点，$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$，过P的直线分别交DA的延长线，AB，DC于M，E，N，若$\overrightarrow{DM}=m\overrightarrow{DA}，\overrightarrow{DN}=n\overrightarrow{DC}$，则2m+3n的最小值是（ ）
如图，矩形ABCD，AB=2，AD=1，P是对角线AC上一点，$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$，过P的直线分别交DA的延长线，AB，DC于M，E，N，若$\overrightarrow{DM}=m\overrightarrow{DA}，\overrightarrow{DN}=n\overrightarrow{DC}$，则2m+3n的最小值是（ ）| A． | $\frac{6}{5}$ | B． | $\frac{12}{5}$ | C． | $\frac{24}{5}$ | D． | $\frac{48}{5}$ |