题目内容

14．已知$\vec a=（{1，3}）$，$\vec b=（{-2，k}）$，且$（{\vec a+2\vec b}）∥（{3\vec a-\vec b}）$，则实数k=-6．

分析 利用向量坐标运算性质、向量共线定理即可得出．

解答 解：$\overrightarrow{a}+2\overrightarrow{b}$=（-3，3+2k），$3\overrightarrow{a}$-$\overrightarrow{b}$=（5，9-k）．
∵$（{\vec a+2\vec b}）∥（{3\vec a-\vec b}）$，∴-3（9-k）-5（3+2k）=0，
解得k=-6．
故答案为：-6．

点评 本题考查了向量坐标运算性质、向量共线定理，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
4．设集合M={x|2x+1＞1}，N={x|lnx≤1}，则M∩N等于（　　）
A．（-∞，e]B．（-1，1]C．（0，1）D．（0，e]
5．设命题P：?n∈N，n2＜2n，则￢P为（　　）
A．?n∈N，n2＜2nB．?n∈N，n2≥2nC．?n∈N，n2≥2nD．?n∈N，n2＞2n
2．用数学归纳法证明不等$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}＞\frac{11}{24}（{n∈{N^*}}）$式的过程中，由n=k递推到n=k+1时，下列说法正确的是（　　）
A．增加了一项$\frac{1}{{2（{k+1}）}}$B．增加了两项$\frac{1}{2k+1}$和$\frac{1}{{2（{k+1}）}}$
C．增加了B中两项，但又少了一项$\frac{1}{k+1}$D．增加了A中一项，但又少了一项$\frac{1}{k+1}$
9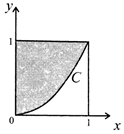．在如图所示的正方形中随机投掷10000个点，则落入阴影部分（曲线C的方程为x2-y=0）的点的个数的估计值为（　　）
A．5000B．6667C．7500D．7854
19．已知点F为椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左焦点，且两焦点与短轴的一个顶点构成一个等边三角形，直线$\frac{x}{4}+\frac{y}{2}=1$与椭圆E有且仅有一个交点M．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设直线$\frac{x}{4}+\frac{y}{2}=1$与y轴交于P，过点P的直线与椭圆E交于两不同点A，B，若λ|PM|2=|PA|•|PB|，求实数λ的取值范围．
6．若x0是方程lnx+x-3=0的实数解，则x0属于区间（　　）
A．（1，1.5）B．（1.5，2）C．（2，2.5）D．（2.5，3）
3．已知函数f（x）=|x-a|．
（Ⅰ）若a=1，解不等式：f（x）≥4-|x-3|；
（Ⅱ）若f（x）≤1的解集为[0，2]，$\frac{1}{m}+\frac{1}{2n}=a$（m＞0，n＞0），求mn的最小值．
4．定义在[0，+∞）上的函数f（x）满足：①当x∈[1，2）时，$f（x）=\frac{1}{2}-|{x-\frac{3}{2}}|$；②?x∈[0，+∞）都有f（2x）=2f（x）．设关于x的函数F（x）=f（x）-a的零点从小到大依次为x1，x2，x3，…xn，…，若$a∈（{\frac{1}{2}，1}）$，则x1+x2+…+x2n=6×（2n-1）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网