题目内容
5.设命题P:?n∈N,n2<2n,则¬P为( )| A. | ?n∈N,n2<2n | B. | ?n∈N,n2≥2n | C. | ?n∈N,n2≥2n | D. | ?n∈N,n2>2n |
分析 直接利用特称命题的否定是全称命题写出结果即可.
解答 解:因为特称命题的否定是全称命题,
所以命题P:?n∈N,n2<2n的否定是?n∈N,n2≥2n;
故选:C
点评 本题考查命题的否定特称命题与全称命题的关系,基本知识的考查.

练习册系列答案
相关题目
15.圆柱被一个平面截去一部分后与一个四棱锥组成的几何体的三视图如图所示,则该几何体的体积为( )
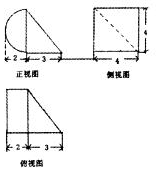

| A. | 4π+8 | B. | 8π+16 | C. | 16π+16 | D. | 16π+48 |
16.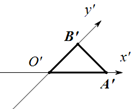 如图一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′,若O′B′=B′A′=1,那么原△ABO的面积是( )
如图一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′,若O′B′=B′A′=1,那么原△ABO的面积是( )
 如图一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′,若O′B′=B′A′=1,那么原△ABO的面积是( )
如图一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′,若O′B′=B′A′=1,那么原△ABO的面积是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
13.下列结论正确的是( )
| A. | 事件A的概率P(A)必有0<P(A)<1 | |
| B. | 事件A的概率P(A)=0.999,则事件A是必然事件 | |
| C. | 用某种药物对患有胃溃疡的500名病人治疗,结果有380人有明显的疗效,现有胃溃疡的病人服用此药,则估计其有明显的疗效的可能性为76% | |
| D. | 某奖券中奖率为50%,则某人购买此券10张,一定有5张中奖 |
20.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 5 | B. | $\frac{16}{3}$ | C. | 7 | D. | $\frac{17}{3}$ |
10.若函数$f(x)={x^2}+ax+\frac{1}{x}$在$({\frac{1}{2}\;\;,\;\;1})$内任取两个实数p,q,且p≠q,不等式$\frac{f(p)-f(q)}{p-q}>0$恒成立,则a的取值范围是( )
| A. | [-1,0] | B. | [-1,+∞) | C. | [0,3] | D. | [3,+∞) |
17.设p:x<4,q:1<x<4,则p是q成立的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既充分也不必要条件 |
15.已知集合P={x|-1≤x≤1},M={a},若P∩M=∅,则a取值范围是( )
| A. | (-∞,-1] | B. | [1,+∞) | C. | [-1,1] | D. | (-∞,-1)∪(1,+∞) |