题目内容
12.已知sinαcosα=$\frac{3}{8}$,且$\frac{π}{4}$<α<$\frac{π}{2}$,则cosα-sinα的值是-$\frac{1}{2}$.分析 求出(cosα-sinα)2=1-2sinαcosα=$\frac{1}{4}$,再判断cosα<sinα,得出答案.
解答 解:∵sinαcosα=$\frac{3}{8}$,
∴(cosα-sinα)2=1-2sinαcosα
=$\frac{1}{4}$,
∵$\frac{π}{4}$<α<$\frac{π}{2}$,
∴cosα<sinα,
∴cosα-sinα=-$\frac{1}{2}$.
点评 考查了三角函数间的关系,属于基础题型,应熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知cosx+sinx=$\frac{{3\sqrt{2}}}{5}$,那么sin2x=( )
| A. | $\frac{18}{25}$ | B. | $-\frac{7}{25}$ | C. | $±\frac{24}{25}$ | D. | $\frac{7}{25}$ |
2.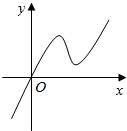 已知函数f(x)的定义域为R,且满足f(4)=1,f′(x)为f(x)的导函数,又知y=f′(x)的图象如图所示,若两个正数a,b满足,f(2a+b)<1,则$\frac{b+2}{a+1}$的取值范围是( )
已知函数f(x)的定义域为R,且满足f(4)=1,f′(x)为f(x)的导函数,又知y=f′(x)的图象如图所示,若两个正数a,b满足,f(2a+b)<1,则$\frac{b+2}{a+1}$的取值范围是( )
 已知函数f(x)的定义域为R,且满足f(4)=1,f′(x)为f(x)的导函数,又知y=f′(x)的图象如图所示,若两个正数a,b满足,f(2a+b)<1,则$\frac{b+2}{a+1}$的取值范围是( )
已知函数f(x)的定义域为R,且满足f(4)=1,f′(x)为f(x)的导函数,又知y=f′(x)的图象如图所示,若两个正数a,b满足,f(2a+b)<1,则$\frac{b+2}{a+1}$的取值范围是( )| A. | $({\frac{2}{3},6})$ | B. | $[{\frac{2}{3},6}]$ | C. | $[\frac{1}{4},\frac{5}{2}]$ | D. | $({\frac{1}{4},\frac{5}{2}})$ |
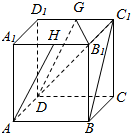 在正方体ABCD-A1B1C1D1中,G是C1D1的中点,H是A1B1的中点
在正方体ABCD-A1B1C1D1中,G是C1D1的中点,H是A1B1的中点