Question

7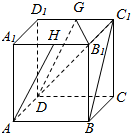．在正方体ABCD-A₁B₁C₁D₁中，G是C₁D₁的中点，H是A₁B₁的中点
（1）求异面直线AH与BC₁所成角的余弦值；
（2）求证：BC₁∥平面B₁DG．

Answer 1

分析 （1）连结AD₁，HD₁，说明∠D₁AH为异面直线AH与BC₁所所成的角，在△AD₁H中，求解cos∠D₁AH的值即可．
（2）证明：连结BD₁交B₁D于点O，连结OG，证明OG∥BC₁，然后证明BC₁∥平面B₁DG

解答 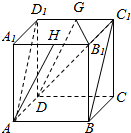解：（1）连结AD₁，HD₁，
∵AB∥C₁D₁  AB=C₁D₁
∴四边形ABC₁D₁为平行四边形，
∴AD₁∥BC₁，
∴∠D₁AH为异面直线AH与BC₁所所成的角，…．…．（2分）
设正方体棱长为1，
在△AD₁H中，AD₁=$\sqrt{2}$，AH=D1H=$\frac{\sqrt{5}}{2}$，
∴cos∠D₁AH=$\frac{{D}_{1}{H}^{2}+{AH}^{2}-{D}_{1}{H}^{2}}{2{D}_{1}H•AH}$=$\frac{\sqrt{10}}{5}$       …..…．（5分）
∴异面直线AH与BC₁所成角的余弦值为$\frac{\sqrt{10}}{5}$           …．（6分）
（2）证明：连结BD₁交B₁D于点O，
连结OG，易知O为BD₁的中点，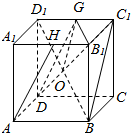

在△BC₁D₁中，OG为中位线，∴OG∥BC₁
又OG?平面B₁DG且SC₁?平面B₁DG，
∴BC₁∥平面B₁DG  …．（12分）

点评 本题考查直线与平面平行的判定定理以及异面直线所成角的求法，考查计算能力．