题目内容
10.已知函数f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$-$\frac{1}{2}$,$\overrightarrow{m}$=($\sqrt{3}$sinx,cosx),$\overrightarrow{n}$=(cosx,-cosx).(1)求函数y=f(x)在x∈[0,$\frac{π}{2}$]时的值域;
(2)在△ABC中,角A、B、C所对的边分别为a、b、c,且满足c=2,a=3,f(B)=0,求边b的值.
分析 (1)根据平面向量的数量积与三角函数的恒等变换,求出f(x)的解析式,再求f(x)在[0,$\frac{π}{2}$]取值范围即可;
(2)利用f(B)=0求出B的值,再由余弦定理求出b的值.
解答 解:(1)∵$\overrightarrow{m}$=($\sqrt{3}$sinx,cosx),$\overrightarrow{n}$=(cosx,-cosx),
∴f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$-$\frac{1}{2}$
=$\sqrt{3}$sinxcosx-cos2x-$\frac{1}{2}$
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x-1
=sin(2x-$\frac{π}{6}$)-1,…4分
∵x∈[0,$\frac{π}{2}$],
∴2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],
∴sin(2x-$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],
∴函数f(x)在[0,$\frac{π}{2}$]的值域为[-$\frac{3}{2}$,0];…8分
(2)因为f(B)=0,即sin(2B-$\frac{π}{6}$)=1,
∵B∈(0,π),∴2B-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{11π}{6}$),
∴2B-$\frac{π}{6}$=$\frac{π}{2}$,解得B=$\frac{π}{3}$;…10分
又有c=2,a=3,
在△ABC中,由余弦定理得:
b2=c2+a2-2accos$\frac{π}{3}$=4+9-2×2×3×$\frac{1}{2}$=7,
即b=$\sqrt{7}$.…14分.
点评 本题考查了平面向量的数量积与三角函数的恒等变换问题,也考查了解三角形的应用问题,是综合性题目.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案| A. | {2,6,8} | B. | {2,4,6,8} | C. | {0,2,4,6,8} | D. | {0,2,6,8} |
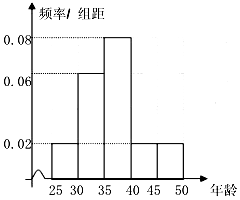 我校名教师参加我县“六城”同创“干部职工进网络,服务群众进社区”活动,他们的年龄均在25岁至50岁之间,按年龄分组:第一组[25,30),第二组[30,35),第三组[35,40),第四组[40,45),第五组[45,50],得到的频率分布直方图如图所示:
我校名教师参加我县“六城”同创“干部职工进网络,服务群众进社区”活动,他们的年龄均在25岁至50岁之间,按年龄分组:第一组[25,30),第二组[30,35),第三组[35,40),第四组[40,45),第五组[45,50],得到的频率分布直方图如图所示:| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 5 | a | b |
(1)求正整数a,b,N的值;
(2)根据频率分布直方图估计我校这N名教师年龄的中位数和平均数;
(3)从第一、二组用分层抽样的方法抽取4人,现在从这4人中任取两人接受咸丰电视台的采访,求从这4人中选取的两人年龄均在第二组的概率.
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
 已知奇函数$f(x)=\left\{{\begin{array}{l}{-{x^2}+2x}\\ 0\\{{x^2}+2x}\end{array}\begin{array}{l}{({x>0})}\\{({x=0})}\\{({x<0})}\end{array}}\right.$
已知奇函数$f(x)=\left\{{\begin{array}{l}{-{x^2}+2x}\\ 0\\{{x^2}+2x}\end{array}\begin{array}{l}{({x>0})}\\{({x=0})}\\{({x<0})}\end{array}}\right.$