题目内容
8.若变量x、y、z满足约束条件$\left\{\begin{array}{l}{\stackrel{x+2y≥0}{x-y≤0}}\\{x-2y+2≥0}\end{array}\right.$,且m∈(-7,3),则z=$\frac{y}{x-m}$仅在点A(-1,$\frac{1}{2}$)处取得最大值的概率为( )| A. | $\frac{2}{7}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{10}$ | D. | $\frac{3}{10}$ |
分析 由约束条件作出可行域,再由z=$\frac{y}{x-m}$的几何意义,即可行域内动点与定点(m,0)连线的斜率求得m的范围,由几何概型概率计算公式得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{\stackrel{x+2y≥0}{x-y≤0}}\\{x-2y+2≥0}\end{array}\right.$作出可行域如图,
z=$\frac{y}{x-m}$的几何意义为可行域内动点与定点(m,0)连线的斜率,
∵z=$\frac{y}{x-m}$仅在点A(-1,$\frac{1}{2}$)处取得最大值,
∴由图可知-2<m<-1.
又m∈(-7,3),
∴z=$\frac{y}{x-m}$仅在点A(-1,$\frac{1}{2}$)处取得最大值的概率为P=$\frac{1}{3-(-7)}=\frac{1}{10}$.
故选:C.
点评 本题主要考查线性规划的应用,结合直线斜率的几何意义是解决本题的关键,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.椭圆$\left\{\begin{array}{l}x=5cosφ\\ y=3sinφ\end{array}\right.(φ为参数)$的焦点坐标为( )
| A. | (±5,0) | B. | (±4,0) | C. | (±3,0) | D. | (0,±4) |
16.已知集合A={x|2<x<4},B={x|x2-4x+3>0},则A∩B=( )
| A. | (2,3) | B. | (3,4) | C. | (1,3) | D. | (2,4) |
13.若集合A={x|x>1},B={x|x(x-3)<0},则A∩B=( )
| A. | [3,+∞) | B. | (0,3) | C. | (1,3) | D. | (0,1) |
17.对某工厂生产的产品进行质量监测,现随机抽取该工厂生产的某批次产品中的5件进行检测,测得其中x,y两种指标的含量的数据如下:
(Ⅰ)当该产品中指标x,y满足x≥75且y≥80时,该产品为优等品,求该产品为优等品的概率;
(Ⅱ)若从该产品中随机抽取2件,求出取的2件产品中优等品数的分布列和数学期望.
| 产品编号 | 1 | 2 | 3 | 4 | 5 |
| 指标 x | 69 | 78 | 66 | 75 | 80 |
| 指标 y | 75 | 80 | 77 | 70 | 81 |
(Ⅱ)若从该产品中随机抽取2件,求出取的2件产品中优等品数的分布列和数学期望.
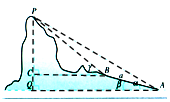 如图,在山脚A测得山顶P的仰角为60°,沿倾斜角为15°的斜坡向上走200米到B,在B处测得山顶P的仰角为75°,则山高h=150($\sqrt{6}$+$\sqrt{2}$)米.
如图,在山脚A测得山顶P的仰角为60°,沿倾斜角为15°的斜坡向上走200米到B,在B处测得山顶P的仰角为75°,则山高h=150($\sqrt{6}$+$\sqrt{2}$)米.