题目内容
15.a=sin$\frac{2π}{7}$,b=cos$\frac{2π}{7}$,c=tan$\frac{2π}{7}$,则( )| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
分析 解法一:根据三角函数的图象与性质,结合cos$\frac{π}{4}$=sin$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$,tan$\frac{π}{4}$=1,即可比较大小;
解法二:用三角函数线分别表示出cos$\frac{2π}{7}$、sin$\frac{2π}{7}$、tan$\frac{2π}{7}$,也可以比较它们的大小.
解答 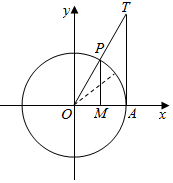 解:(解法一)∵$\frac{π}{4}$=$\frac{2π}{8}$<$\frac{2π}{7}$<$\frac{π}{2}$,
解:(解法一)∵$\frac{π}{4}$=$\frac{2π}{8}$<$\frac{2π}{7}$<$\frac{π}{2}$,
∴cos$\frac{2π}{7}$<sin$\frac{2π}{7}$<1<tan$\frac{2π}{7}$,
∴b<a<c.
(解法二)用三角函数线表示如下;
cos$\frac{2π}{7}$=$\overrightarrow{OM}$,sin$\frac{2π}{7}$=$\overrightarrow{MP}$,tan$\frac{2π}{7}$=$\overrightarrow{AT}$;
且$\frac{π}{2}$>$\frac{2π}{7}$>$\frac{π}{4}$,
∴|$\overrightarrow{OM}$|<|$\overrightarrow{MP}$|<|$\overrightarrow{AT}$|,
∴b<a<c.
故选:D.
点评 本题考查了三角函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
17.已知sinθ=$\frac{3}{5}$,θ∈(${\frac{π}{2}$,π),则tan(θ+$\frac{π}{4}$)=( )
| A. | -7 | B. | 7 | C. | $-\frac{1}{7}$ | D. | $\frac{1}{7}$ |