题目内容
6.已知函数f(x)=cos(2x+φ)的图象关于点($\frac{2}{3}$π,0)对称,若将函数f(x)的图象向右平移m(m>0)个单位得到一个偶函数的图象,则实数m的最小值为$\frac{π}{12}$.分析 利用余弦函数的对称性可得φ=kπ-$\frac{5π}{6}$,k∈Z,利用函数y=Asin(ωx+φ)的图象变换规律及余弦函数的奇偶性解得m=$\frac{(k-{k}_{1})π}{2}$-$\frac{5π}{12}$,结合m的范围,即可得解最小值.
解答 解:∵函数f(x)=cos(2x+φ)的图象关于点($\frac{2}{3}$π,0)对称,
∴2×$\frac{2π}{3}$+φ=kπ+$\frac{π}{2}$,k∈z,解得:φ=kπ-$\frac{5π}{6}$,k∈Z,
∴f(x)=cos(2x+kπ-$\frac{5π}{6}$),k∈Z,
∵将函数f(x)的图象向右平移m(m>0)个单位得到函数y=cos[2(x-m)+kπ-$\frac{5π}{6}$]=cos(2x-2m+kπ-$\frac{5π}{6}$),k∈Z为偶函数,
∴要使函数g(x)为偶函数,即x=0为其对称轴,只需-2m+kπ-$\frac{5π}{6}$=k1π,(k∈Z,k1∈Z),
∴解得:m=$\frac{(k-{k}_{1})π}{2}$-$\frac{5π}{12}$,
∵m>0
∴m的最小正值为$\frac{π}{12}$,此时k-k1=1,k∈Z,k1∈Z.
故答案为:$\frac{π}{12}$.
点评 本题主要考查了余弦函数的图象和性质,函数y=Asin(ωx+φ)的图象变换规律,考查了数形结合思想和转化思想,属于中档题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
14.抛物线y2=8x的焦点为F,其准线与x轴的交点为Q,过点F作直线与此抛物线交于A,B两点,若$\overrightarrow{FA}$•$\overrightarrow{QB}$=0,则|AF|-|BF|=( )
| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
1.若命题p:?x∈R,不等式x2-2$\sqrt{2}$x+a>0恒成立,命题q:?x∈R,不等式|x-1|+|x+1|>a恒成立,则命题¬p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
15.a=sin$\frac{2π}{7}$,b=cos$\frac{2π}{7}$,c=tan$\frac{2π}{7}$,则( )
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
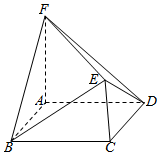 如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.
如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.