题目内容
14.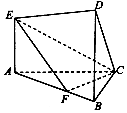 在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB(1)求证:CF⊥EF;
(2)求二面角D-CE-F的余弦值.
分析 (1)求出AB=3$\sqrt{3}$,FB=$\sqrt{3}$,从而推导出CF⊥AB,EA⊥平面ABC,由此能证明CF⊥EA.
(Ⅱ)连结DF,推导出DF⊥EF,DF⊥CF,从而DF⊥平面EFC,进而DF⊥EC,过D作DG⊥EC于G,则EC⊥平面DFG,连结FG,则EC⊥FG,∠DGF是二面角D-CE-F的平面角,由此能求出二面角D-CE-F的余弦值.
解答 证明:(1)∵AC=3$\sqrt{2}$,BC=3,AC⊥BC,∴AB=3$\sqrt{3}$,
∵AF=2FB,∴FB=$\sqrt{3}$,
又cosB=$\frac{BC}{AB}$=$\frac{3}{3\sqrt{3}}$=$\frac{1}{\sqrt{3}}$,
∴CF2=BC2+BF2-2BC×BF×cosB=6,
∵CF2+BF2=BC2,∴CF⊥AB,
∵EA⊥平面ABC,CF?平面ABC,∴CF⊥EA.
解:(Ⅱ)连结DF,在Rt△EAF中,EF=$\sqrt{A{E}^{2}+A{F}^{2}}$=$\sqrt{4+12}$=4,
在Rt△DBF中,DF=$\sqrt{B{F}^{2}+B{D}^{2}}$=$\sqrt{3+9}$=2$\sqrt{3}$,
在直角梯形EABD中,ED=$\sqrt{A{B}^{2}+(BD-AF)^{2}}$=$\sqrt{27+(3-2)^{2}}$=2$\sqrt{7}$,
∵ED2=EF2+DF2,∴DF⊥EF,
∴CF⊥平面EABD,∴DF⊥CF,
∵EF∩CF=F,∴DF⊥平面EFC,∴DF⊥EC,
过D作DG⊥EC于G,则EC⊥平面DFG,
连结FG,则EC⊥FG,
∴∠DGF是二面角D-CE-F的平面角,
在Rt△EFC中,FG=$\frac{FC×FE}{EC}$=$\frac{4\sqrt{6}}{\sqrt{22}}$,
在Rt△DFG中,cos$∠DGF=\frac{FG}{DG}$=$\frac{2\sqrt{15}}{15}$,
∴二面角D-CE-F的余弦值为$\frac{2\sqrt{15}}{15}$.
点评 本题考查线线垂直的证明,考查二面角的余弦值的求法,涉及到空间中线线、线面、面面间的位置关系等知识点,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.

| A. | $\frac{{\sqrt{3}}}{4}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | 9 |
| A. | $\frac{{\sqrt{3}}}{15}$ | B. | $\frac{{\sqrt{3}}}{16}$ | C. | $\frac{{\sqrt{2}}}{16}$ | D. | $\frac{{\sqrt{2}}}{14}$ |
| A. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}+1}{4}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
| A. | [-1,$\frac{1}{2}$] | B. | [-$\frac{1}{4}$,$\frac{1}{2}$] | C. | [-$\frac{5}{3}$,+∞) | D. | (-∞,-$\frac{5}{3}$] |
| A. | $\frac{\sqrt{13}}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
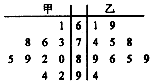 甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.
甲、乙两位同学参加数学竞赛培训,培训期间共参加了10次模拟考试,根据考试成绩,得到如图所示的茎叶图.